Relativity and Black Holes
Classical Mechanics
Though the contributions to science and math from classical Greece are
extensive, some ideas from this period far outlived their usefulness.
Aristotle, preferring to base his ideas on pure logic instead of
experiment, came up with a number of incorrect ideas in mechanics. He
theorized that heavy objects fall faster than light objects, that objects
in motion can only remain in motion by being given some sort of push, and
that the Earth is the center of the universe. Unfortunately, the Christian
church adopted Aristotle's ideas and they persisted for over 1500 years.
The Polish astrologer/astronomer Nicholas Copernicus popularized the idea
of a Sun-centered universe. His arguments were based on the simplification
of the observed motions of the planets and eliminated Aristotle's complex
system of epicycles.
Johannes Kepler is sometimes called the last professional
astrologer/ astronomer. He frequently made money by casting horoscopes,
but spent most of his life looking for a mathematical model (sometimes
based on mystical notions) to describe the motions of the planets.
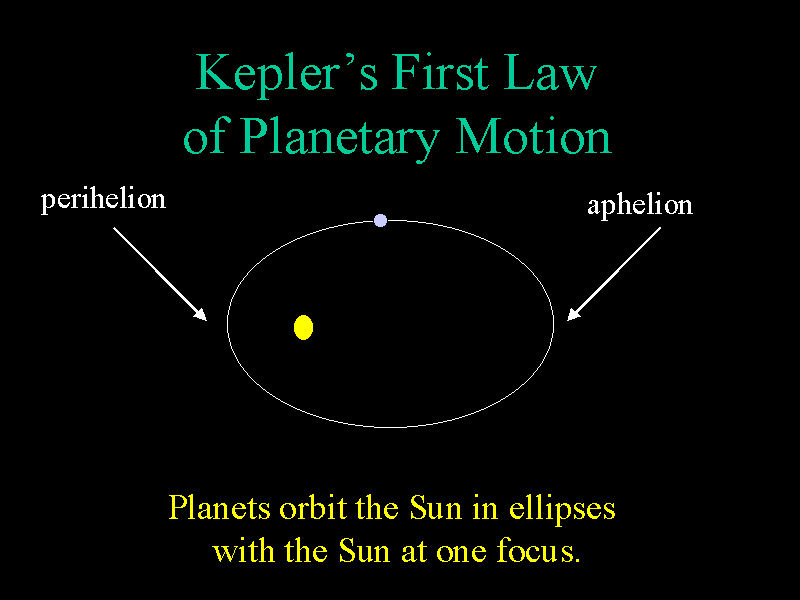Without
any physical reasons, Kepler came up with his famous three laws of
planetary motion. Of primary concern to us today, is his first law which
states that a planet orbits the Sun in an elliptical orbit with the
Sun at one focus.
Galileo completely abandoned the theological approach to mechanics, and
experimentally laid down much of the foundations of classical physics. Above
all others, it is Galileo who put an end to Aristotelean mechanics. In
addition, Galileo invented the first telescope. With it, he discovered
craters on the moon and 4 satellites in orbit around Jupiter; both
observations which contradicted Aristotle. He also discovered the phases
of Venus which offered confirmation of Copernicus' heliocentric theory.
Sir Isaac Newton was center-stage for the golden age of classical
mechanics. He laid the foundations for calculus and then used this new
branch of math to show that an inverse square law of gravitation implies
Kepler's laws of planetary motion. The tremendous success of Newtonian
mechanics lulled many 19th century physicists into a false sense of
security and had some of them proclaim that the "end of physics is near."
(These comments seem ludicrous today, since they preceded relativity and
quantum theory.) In a nutshell, Newton's contributions to mechanics can be
summarized in his three laws of motion.
In particular, Newton's first law (also called the Law of Inertia)
states that a body at rest remains at rest and a body in motion remains in
motion... unless acted upon by an outside force. This is in clear
contradiction to Aristotle.
Newton viewed space as
- unbounded and infinite,
- 3-dimensional and explained by Euclidean geometry, and
- "always similar and immovable."
Newton's laws and ideas of absolute space lead to the idea of the following
transformation, named in honor of Galileo.
If we have two coordinate systems moving as illustrated here, then we can use
the simple idea that distance equals rate times time to conclude that the
coordinates are related by the equations:
x=x'+vt, y=y', z=z', and t=t'.
Strangely enough, however, there are settings in which Newton's laws are
insufficient and his view of absolute space is wrong! In these settings,
the Galilean transformation is not sufficient and we need a more sophisticated
theory of mechanics!
Go to next section.