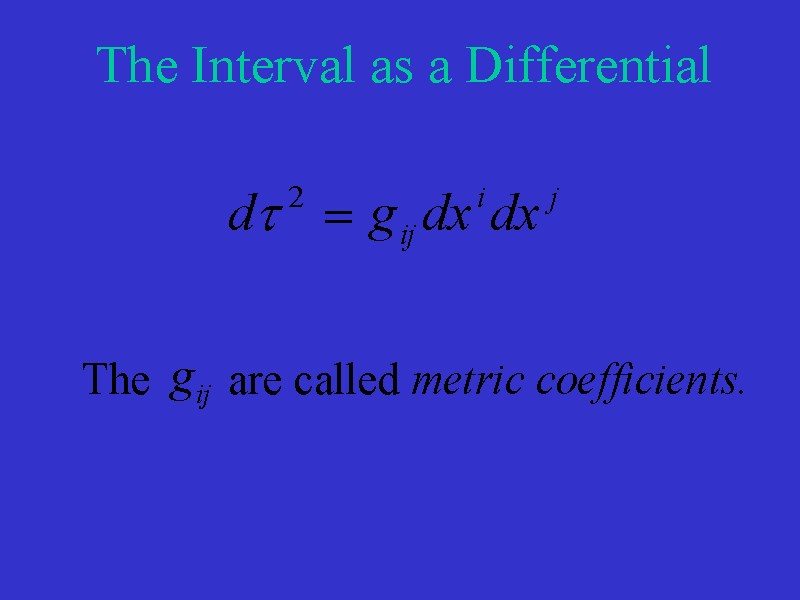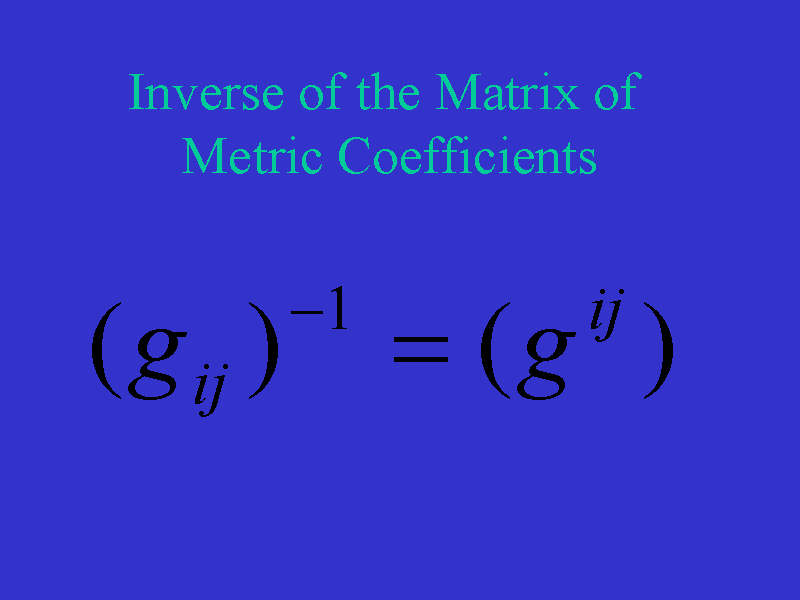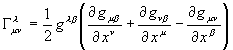Relativity and Black Holes
General Relativity
Einstein was bothered by what he saw as a dichotomy in the concept of
"mass."
On one hand, by Newton's second law (F=ma), "mass" is treated as a measure
of an objects resistance to changes in movement. This is called inertial
mass. On the other hand, by Newton's Law of Universal Gravitation, an object's
mass measures its response to gravitational attraction. This is called
gravitational mass. As we will see, Einstein resolves this dichotomy by
putting gravity and acceleration on an equal footing.
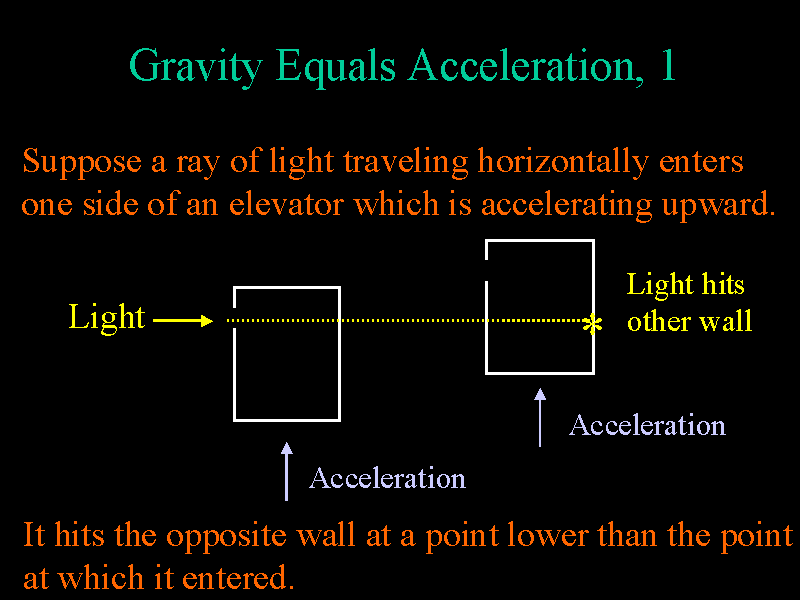Consider an observer in a windowless elevator which is accelerating upward.
Suppose a ray of light enters near the top of the elevator on one side.
Then while the light travels from one side of the elevator to the other,
the elevator will accelerate upward and therefore the light will hit the
opposite wall at a point lower than the point at which it entered.
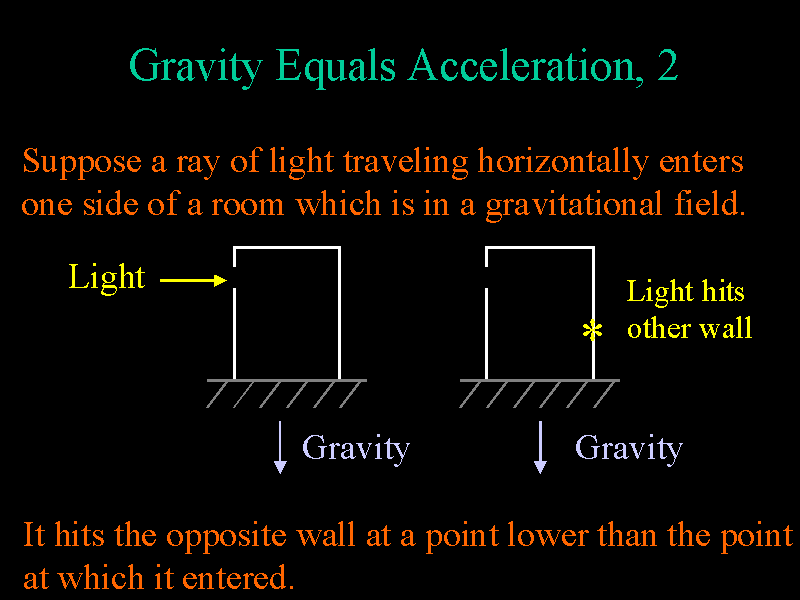Next, suppose the elevator is
stationary, but in a gravitational field. Then if we put gravity and
acceleration on an equal footing, we would expect the same outcome of our
experiment involving light rays. That is, if a ray of light enters near the
top of the stationary elevator on one side, we expect the light to hit the
opposite wall at a point lower than the point at which it entered the elevator.
In a sense, the light "falls" under the influence of gravity. Notice, then,
that an occupant of the elevator could not tell if he were in a rapidly
accelerating elevator, or if he were in a stationary elevator in a
gravitational field.
Einstein summarizes this in his
Principle of Equivalence: There is no way to distinguish between the
effects of acceleration and the effects of gravity - they are equivalent!
In our technical exploration of general relativity, we
will adopt Einstein's summation notation in which an
index of summation appears in each term both as a subscript and as a
superscript and the sigma summation symbol is omitted. Therefore, the sum
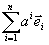becomes just 
.
The double sum 
becomes simply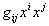 
. The range of the index
of summation will be clear from the context (usually 0 to 3).
In our standard 3-dimensional Euclidean space, we measure the distance
between two points as
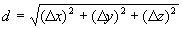If instead of using x, y, z to represent coordinates, we
use x1, x2, x3,
then with Einstein's summation notation, distance
is calculated as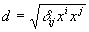 
where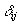 
is the Kronecker delta which takes on the value 1
if i and j are equal and the value 0 if i and
j are different.
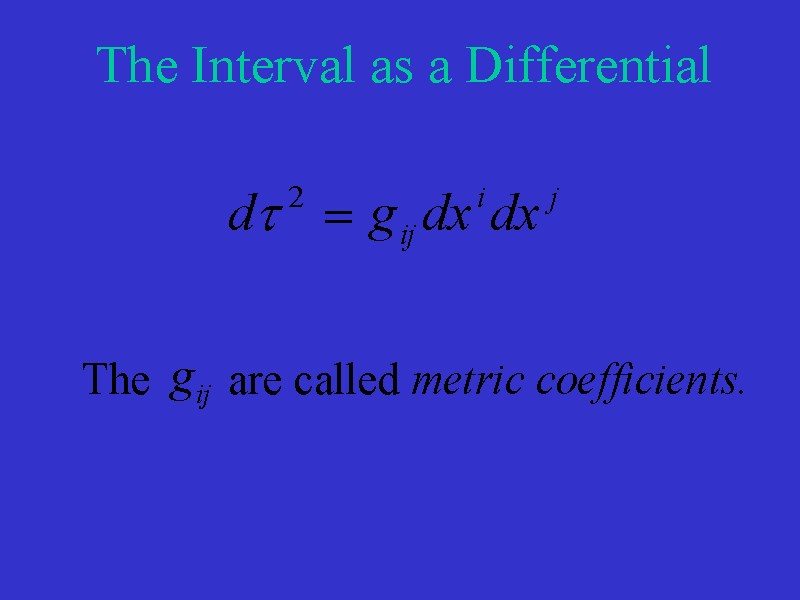Instead of simply measuring the distance between points in spacetime, we will
be interested in differentials of the interval and the coordinates of
spacetime. In a "curved" spacetime, we will measure the quantity as
.
The curvature of the space will
be determined by the gij (which are called metric
coefficients)
and the gij will be functions of space, time, and mass
distribution.
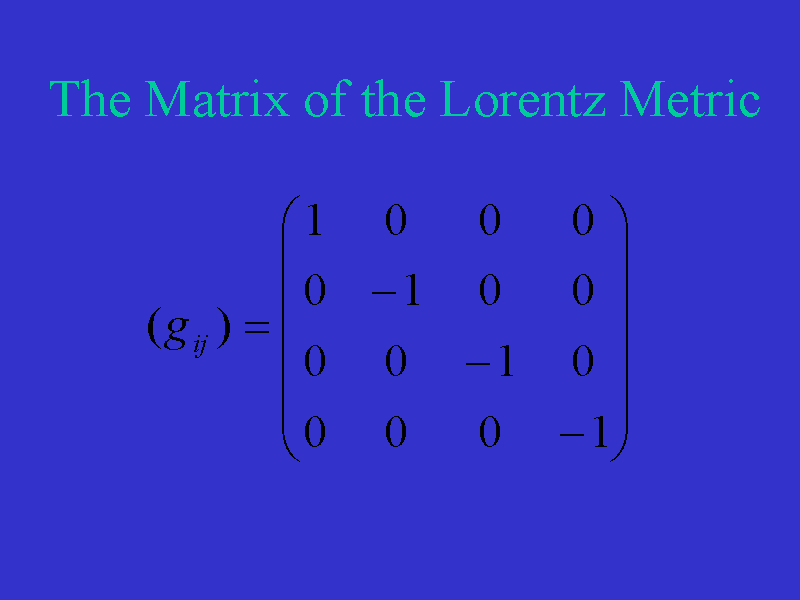As we have seen, in the absence
of matter and with
(t,x,y,z) =
(x0,x1,x2,x3)
the metric coefficients
determine the matrix of the Lorentz metric seen here.
Now let's introduce some of the notation required to understand Einstein's
field equations.
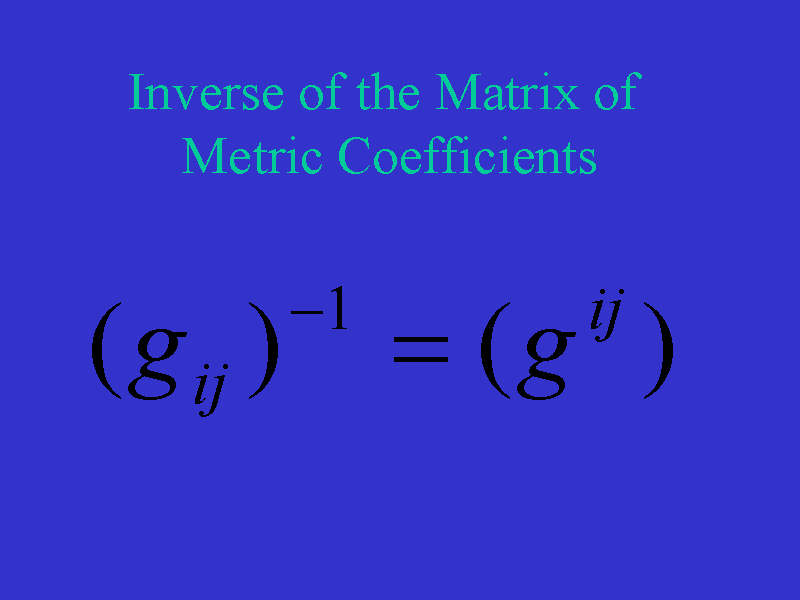First, we define the entries of the inverse of the matrix of metric
coefficients as gij. The gij
and gij and their partial
derivatives are used to define the Christoffel symbols,
.
Notice that these are functions of the gij's and partial
derivatives of the gij's:
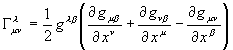
The Ricci tensor is defined, in turn, in terms of the
Christoffel symbols as
seen here.
Einstein chose as his field equations of general relativity, the following:
That is, he chose for his field equations to set the Ricci tensor equal to zero.
Since mu and nu range from 0 to 3, there are 16 different equations here.
We can simplify this notationally as:
So we see that Einstein's field equations are a system of
16 second order partial differential equations in the 16 unknown functions
gij.
Here we see Einstein posing with
his field equation.
The gij determine the metric form of spacetime and therefore all {\it
intrinsic} properties of the 4-dimensional spacetime in which we live. In
particular, curvature is determined by the Riemann-Christoffel curvature
tensor.
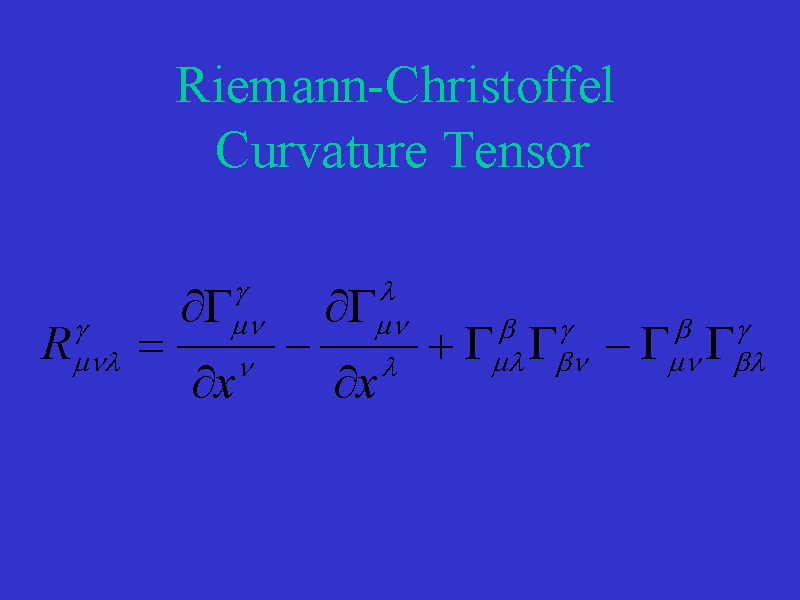Notice that mu, nu, lambda, and gamma range from 0 to 3 and therefore
the curvature tensor consists of 256 entries, only 20 of which are independent.
Go to next section.