Problems

#03

The key equation is that

$$\frac{L}{L_\odot} = \left(\frac{R}{R_\odot}\right)^2 \left( \frac{T}{T_\odot}\right)^4$$

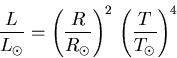
In this problem we have a star that is 3 times bigger than the Sun, so the first parenthetical factor gives 9. The solar temperature is 5800 K, and the star of interest is 10,000 K. That is a ratio of 1.7. Taking the fourth power, the second parenthetical factor is 8.3. Combining, the luminosity of the star is about 75 times greater than the Sun.

#05

Apparent brightness in terms of flux is $F=L/4\pi d^2$. If they have the same flux but different luminosities, this can only be true if they are at different distances. The more luminous one (B) must be farther away (if they were at the same distance, the more luminous star would appear brighter). Since $F_A=F_B$, we have the relation that

$$\frac{L_A}{4\pi d_A^2} = \frac{L_B}{4\pi d_B^2}$$

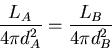
Cancelling the constants, and cross-multiplying gives

$$\frac{d_A^2}{d_B^2} = \frac{L_A}{L_B}=\frac{0.5}{4.5}=1/9$$

This means that B is 3 times farther away than A.

#12

Let's call the bright star ``A'' and the faint star ``B''. With no eclipse, you see the total light from $A+B$. With A in front, there is a 1% drop. That must mean that star A accounts for 99% of the total light. Now when B goes in front, the drop is 10%. Does this mean that star B accounts for 90% of all the light? Doesn't seem to add up.

Look at Fig 17.21. In that figure the brighter star is also bigger. And here is the key. The problem says that the stars are on the main sequence, and so the more luminous star is both more massive and larger in size. When A eclipses B, none of B can be seen, and star A does indeed account for 99% of the combined light. When B eclipses A, behold, part of star A can still be seen, and the drop is only 10%.

What we have is a geometry problem. We must set up an equation that relates the amount of light seen to the geometry. From the eclipse of B by A, we have that

$$\frac{L_B}{L_A} = \frac{1}{99}$$

In the other case of B eclipsing A, the amount of light seen is 90% of the combined light, or $0.9 (L_A+L_B)$. But what does this consist of? Using Fig 17.21, we can see all of star B, so that contributes a luminosity of $L_B$. How much of the A star can we see? Well, we see all but the part covered by star B. The missing fraction (i.e., the fraction of $L_A$ that we cannot see because it is behind star B) is given by the ratio of the circular areas of B to A, or $R_B^2/R_A^2$. If that is the missing fraction, then fraction we do see is just $1-(R_B^2/R_A^2)$. So for example, if star B covers 6% of star A, then we see 94% of star A when B in front of it. Those are just made up numbers. Let's find the actual ones.

What we have then is the following equation: 90% of the total light $L_A+L_B$ is seen, but this equals all of $L_B$ plus a fraction (given above) of $L_A$, so the relation is

$$0.9 (L_A+L_B) = L_B + \left(1+\frac{R_B^2}{R_A^2}\right) L_A$$

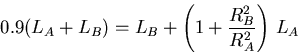
The cute thing about this problem is that we never need to find the actual values of luminosities, radii, or masses for these stars, just their ratios. What we know is that $L_B/L_A=1/99$, so let's divide the equation we have just formed by $L_A$ so that we have luminosity ratios everywhere. This gives:

$$0.9 \left(1+\frac{L_B}{L_A}\right) = \frac{L_B}{L_A}+ \left(1+\frac{R_B^2}{R_A^2}\right)$$

We need to solve for the ratio of radii. Why? Because we are told that $R\propto M$ for stars on the main sequence, hence $R_B/R_A = M_B/M_A$. The ratio of radii is equivalent to the ratio of masses.

This equation looks complicated, but if we said that $x=L_B/L_A$ and $y=R_B/R_A$, the equation would become

$$0.9 (1+x) = x + (1+y^2)$$

Look a little easier? Just solve for $y$.

OK, let's think for a moment. The value of $x$ is 1/99. That is really really small. For example, $1+x \approx 1$ to good accuracy. Thinking in these terms, the equation really looks more like $0.9 = 1+y^2$, or $y=\sqrt{1-0.9}=\sqrt{0.1} \approx 0.3$. This means that star B is only 30% as large (or 70% smaller) than star A. The ratio of the masses is the same.

This was a hard problem, maily because it involves several steps. You will never see anything this challenging on the exam. Still, the problem is not overly complicated. Nothing beyond simple algebra was needed, and it does reflect the kinds of things that real astronomers do. The important lesson is relating a picture of eclipses to formulating an equation that quantifies the geometry in the picture. Fun stuff!