- #01
- We are told that there are
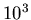 H atoms/m
H atoms/m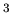 in the Local
Bubble, typically. The mass of one H atom is
in the Local
Bubble, typically. The mass of one H atom is
 kg.
We want to know the mass of a typical volume in the Local Bubble equal
to the volume taken up by the Earth. So find the volume of the Earth.
Multiple by the number density of the Local Bubble to get the number of
H atoms that would normally occupy that volume. Then multiple by the
mass of 1 H atom to get the mass in that volume.
kg.
We want to know the mass of a typical volume in the Local Bubble equal
to the volume taken up by the Earth. So find the volume of the Earth.
Multiple by the number density of the Local Bubble to get the number of
H atoms that would normally occupy that volume. Then multiple by the
mass of 1 H atom to get the mass in that volume.
The first step is that the volume of the Earth (being a sphere) is  . The Earth radius is
. The Earth radius is
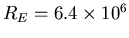 m, so the
volume is
m, so the
volume is
 m
m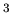 . The number of H atoms in such
a volume for the Local Bubble is
. The number of H atoms in such
a volume for the Local Bubble is
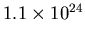 . The mass then is
a mere
. The mass then is
a mere 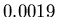 kg, or about 2 grams. Pretty small!
kg, or about 2 grams. Pretty small!
- #02
- Same approach as last problem, just a different volume to
consider. From Table 5 in the appendix, Alpha Cen is at a distance of
1.35 parsecs. The volume of a cylinder is its length times the
cross-sectional area. The distance is the length, and the cross-section
is given at 1 m
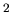 . Let's convert the distance to meters and find the
volume.
. Let's convert the distance to meters and find the
volume.
The distance is
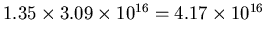 m,
so the volume of the cylinder is
m,
so the volume of the cylinder is
 m
m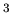 .
.
The number of atoms is thus
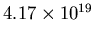 , and the mass is only
, and the mass is only
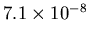 kg.
kg.
- #03
- From Section 18.1, the average number density of the ISM
is
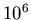 H atoms/m
H atoms/m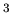 . The average density is then
. The average density is then
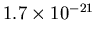 kg/m
kg/m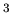 . The density of air at Earth is 1.2 kg/m
. The density of air at Earth is 1.2 kg/m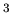 . The question is,
how much ISM volume would have to be compressed to get the same mass
density as air at Earth.
. The question is,
how much ISM volume would have to be compressed to get the same mass
density as air at Earth.
Let's rephrase. If 1 m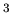 of air at Earth has 1.2 kg of mass, when
volume in the ISM is required to get a total of 1.2 kg of mass? That
is easy - we take 1.2 kg and divide by the density of the ISM gas,
which gives
of air at Earth has 1.2 kg of mass, when
volume in the ISM is required to get a total of 1.2 kg of mass? That
is easy - we take 1.2 kg and divide by the density of the ISM gas,
which gives
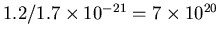 m
m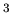 . This
is equivalent to a cube that is about 9,000 km on each side!
. This
is equivalent to a cube that is about 9,000 km on each side!
- #13
- This makes use of the Doppler formula. For wavelengths we
use
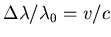 , where
, where 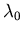 is 21.1 cm, and
for frequencies we use
is 21.1 cm, and
for frequencies we use
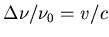 , where
, where 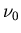 is 1420 MHz. The range of velocities is 75 km/s for receding and
50 km/s for approaching.
is 1420 MHz. The range of velocities is 75 km/s for receding and
50 km/s for approaching.
Let's do wavelengths first. The biggest redshift from 21.1 cm will
be
 cm, and the biggest
blueshift will be
cm, and the biggest
blueshift will be
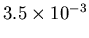 cm, so the range will be from 21.1
cm minus 0.0035 cm to 21.1 cm plus 0.0053 cm.
cm, so the range will be from 21.1
cm minus 0.0035 cm to 21.1 cm plus 0.0053 cm.
Similarly the frequency shifts are 0.35 MHz (redshift) and 0.24 MHz
(blueshift), so the frequency range is from 1420 minus 0.35 MHz to 1420
plus 0.24 MHz.
The trick is to get the adding and subtracting sense correct. Blueshifts
make wavelength shorter but frequencies larger.
- #14
- Rather similar to problem #3. We need the mass of the Sun
and the mass density of the ISM, but we are given the number density.
Look up the mass of the Sun to get
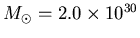 kg.
The number density of H atoms is given as
kg.
The number density of H atoms is given as 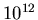 atoms/m
atoms/m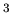 . The mass
density is then
. The mass
density is then
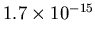 kg/m
kg/m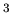 . Dividing the mass density
into the Sun's mass gives the volume
. Dividing the mass density
into the Sun's mass gives the volume 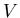 of a molecular cloud of one solar
mass, or
of a molecular cloud of one solar
mass, or
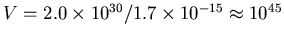 m
m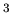 . We are asked to get the cloud's radius. The volume for a sphere
is
. We are asked to get the cloud's radius. The volume for a sphere
is 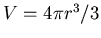 . Solving for the radius gives
. Solving for the radius gives
![$r = \sqrt[3]{3V/4\pi}
\approx 2 \times 10^{14}$](img196.png) m. This is only about 0.01 parsecs.
m. This is only about 0.01 parsecs.
![]() . The Earth radius is
. The Earth radius is
![]() m, so the
volume is
m, so the
volume is
![]() m
m![]() . The number of H atoms in such
a volume for the Local Bubble is
. The number of H atoms in such
a volume for the Local Bubble is
![]() . The mass then is
a mere
. The mass then is
a mere ![]() kg, or about 2 grams. Pretty small!
kg, or about 2 grams. Pretty small!
![]() m,
so the volume of the cylinder is
m,
so the volume of the cylinder is
![]() m
m![]() .
.
![]() , and the mass is only
, and the mass is only
![]() kg.
kg.
![]() of air at Earth has 1.2 kg of mass, when
volume in the ISM is required to get a total of 1.2 kg of mass? That
is easy - we take 1.2 kg and divide by the density of the ISM gas,
which gives
of air at Earth has 1.2 kg of mass, when
volume in the ISM is required to get a total of 1.2 kg of mass? That
is easy - we take 1.2 kg and divide by the density of the ISM gas,
which gives
![]() m
m![]() . This
is equivalent to a cube that is about 9,000 km on each side!
. This
is equivalent to a cube that is about 9,000 km on each side!
![]() cm, and the biggest
blueshift will be
cm, and the biggest
blueshift will be
![]() cm, so the range will be from 21.1
cm minus 0.0035 cm to 21.1 cm plus 0.0053 cm.
cm, so the range will be from 21.1
cm minus 0.0035 cm to 21.1 cm plus 0.0053 cm.