Problems

#01

Our data consist of a mass $M=10^3M_\odot$, radius 10 pc, and temperature $T=10$ K. We need to compute the escape speed and thermal speed for this H cloud.

First the escape speed is

$$v_{esc} = \sqrt{\frac{2GM}{r}}$$

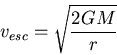
Plugging in the numbers gives $v_{esc} = \sqrt{2 \times 6.67\times 10^{-11} \times 2\times 10^{30} / 10 / 3\times 10^{16} } = 30$ m/s.

The thermal speed can be found using More Precisely 8-1, giving $v_{th} = 0.157 \sqrt{T} = 0.5$ km/s, or 500 m/s.

The thermal speed is much larger larger than the escape speed, so the cloud will not collapse. Mainly this is because the cloud is not especially massive, and is rather extended.

#09

We make use of the equation

$$\frac{L}{L_\odot} = \left(\frac{R}{R_\odot}\right)^2 \left( \frac{T}{T_\odot}\right)^4$$

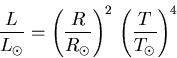
We have that the Brown Dwarf is 0.1 as hot as the Sun and 0.1 as large. Its luminosity relative to the Sun's will be $0.1^2 \times 0.1^4 = 0.1^6 = 10^{-6}$, or 1 millionith as luminous.