The Sun will live for 10 billion years on the main sequence, and the
luminosity 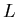 of a star on the main sequence depends on the 4th power
of a star's mass, or
of a star on the main sequence depends on the 4th power
of a star's mass, or 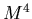 . Now the lifetime also depends on mass, with
. Now the lifetime also depends on mass, with
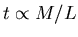 . Since
. Since 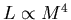 , this means the main sequence
lifetime goes as
, this means the main sequence
lifetime goes as
 . So as the mass goes up,
the lifetime decreases as the cube of mass. So the Sun is
. So as the mass goes up,
the lifetime decreases as the cube of mass. So the Sun is 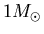 and will live for
and will live for 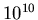 years, hence the lifetime
years, hence the lifetime  for any other
star will be
for any other
star will be
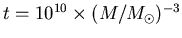 years. This makes
sense, since more massive stars are expected to live shorter lives.
years. This makes
sense, since more massive stars are expected to live shorter lives.
The problem is giving us cluster ages and asking us to find the mass
of the star just leaving the main sequence. So we have to turn the
equation around to find mass in terms of age. This means taking the
quarter power of both sides of the equation, giving
(a) For 400 million years, the mass will be
![$M/M_\odot =
\sqrt[3]{10^{10}/4\times10^8} \approx 3$](img220.png) , or 3 solar masses.
, or 3 solar masses.
(b) Now
![$M/M_\odot = \sqrt[3]{10^{10}/4\times10^9} = 1.7$](img221.png) ,
or 1.7 solar masses.
,
or 1.7 solar masses.
![\begin{displaymath}\frac{M}{M_\odot} = \sqrt[3]{\frac{10^{10}}{t}} \end{displaymath}](img219.png)
![]() , or 3 solar masses.
, or 3 solar masses.
![]() ,
or 1.7 solar masses.
,
or 1.7 solar masses.