Problems

#01

Brightness is described by the flux $f$ of light, given by the equation $f=L/4\pi d^2$. The SN and sun have the same flux, but the sun is at 10 kpc, and the luminosity of the SN is $10^9$ larger than the sun's. Since the fluxes are the same, we have that

$$frac{10^9L_\odot}{d^2} = \frac{L_\odot}{(10\;{\rm kpc})^2}$$

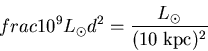
Cross-multiplying to solve for $d$ gives, $d= 10\;{\rm kpc}\; \sqrt{10^9} \approx 300,000$ kpc.

#03

The Hubble law is $v=Hd$, so the first part is $v=70\times 200 = 14,000$ km/s. Turning it around to find $d$, the relation is $d=v/H$. For $v=4000$ km/s, the distance is $d=4000/70 \approx 60$ Mpc. For $H=60$, the answers change to $12,000$ km/s and about 70 Mpc. For $H=80$, they are 16,000 km/s and 50 Mpc.

#11

Angular size $\theta$ is given approximately by the formula $\theta = D/d$, where $D$ is the physical size, and $d$ is distance. We have that $D=1$ Mpc and $d=4$ Mpc, so $\theta=0.25$ radians. The size of the Moon is about 0.5 degrees, so we need to convert radians to degrees. There are 57.3 degrees in 1 radian, so the radio lobes of Cen A are about 14 degrees - much larger than the angular size of the Moon (almost 30 times bigger!).

#12

The equation for flux is $f=L/4\pi d^2$, and we given that $L=10^{37}$ Watts, and that $d=8$ kpc. Converting the distance to meters, we have $d=2.4 \times 10^{19}$ m. Plugging into the flux formula yields $f=10^{37}/4/\pi/ (2.4\times 10^{20})^2\approx 10^{-5}$ W/m$^2$.

Sirius has $L=22L_\odot$ and a distance $d=2.64$ pc. Its flux at Earth is $f=22\times 3.86\times 10^{26}/4/\pi/(2.64\times3\times10^{16})^2 = 10^{-7}$ W/m$^2$, about 100 times smaller than the Seyfert.

Ignoring interstellar extinction is probably not appropriate. A lot of the emission from active galaxies comes out at radio and hard X-ray wavelengths, which can easily pass through interstellar gas and dust without much extinction. However a lot of light is generated in the IR and particularly the optical and UV, and these are influenced by extinction. The extinction can come from gas and dust in our Galaxy, or in the galaxy where the emission is generated, and even in the extended accretion disk around the black hole.