Problems

#08

The number $N$ of technological civilizations is given by the product of a number of factors. (see pg 751, bottom). If the star formation rate is 20 per year, and all of the probably factors are 1/10, then we have that $N = 2\times 10^{-4} t$, where $t$ is the lifetime of a civilization. So the answers are
(a) $N=0.02$
(b) $N=2$
(c) $N=200$

#09

This is the most subtle problem given in this semester, but it is very interesting. The two-communication time can be made arbitrarily short by just having the galaxy full of lots and lots of aliens. Actually, the main limit would be the distanct to the nearest star, which is about 4 LYs, so two-way communication would take 8 years.

The problem wants to know, in effect, what is the minimum number of civilizations required in the galaxy so that we could communicate with them within the average lifetime of a civiliation with our nearest neighbor. So, if we send out a signal, what is the lifetime and number of civilizations required so that we get a response before we die.

First, we adopt the idea that the number of civilizations $N$ equals the average life time $t$, or $N=t/t_0$. Here $t_0$ equals just one year and is there to make the units come out (since $N$ is just a number without units, so we require $t$ in years).

So the average surface density of these civilized worlds will be $N/A_{\rm tot}$, where $A_{\rm tot}$ is the area of the galactic disk. If we take the disk as circular with a radius $R$, then the average density is $N/\pi R^2$.

So how close is the nearest civilization? Let's approach it this way. On average, how much galactic space (i.e., area) is on average associated with a given civilized world. That means that the density times the area gives just one civilization, or $A \times N/\pi R^2 = 1$. This area is circular with radius $l$, so that $\pi l^2 \times N/\pi R^2 = 1$, or

$$l^2 = R^2/N$$

This means the distance to the nearest civilized planet is $2l$. The light travel time for communication is $t = 4l/c$ (because we send a signal, and then they send reply). We can rewrite this as $l=ct/4$

Now $t$ is the communication time, but we want that equal to the civilization lifetime. We know that $N$ is related to $t$, $l$ is related to $t$, and $l$ is related to $N$. Let's take the equation line above, substitute for $l$ to get $t$, and $N$ to get $t$, and we have that

$$(ct/4)^2 = \frac{R^2}{(t/t_0)}$$

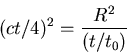
Use algebra to solve for $t$, giving

$$t^3 = \frac{16 R^2 t_0}{c^2}$$

Plug in the numbers and take the cube root (remember to convert $t_0$ from 1 year to seconds), and one gets $t\approx 3300$ years, or over 3 millenia.

#11

The total travel distance is there and back, so 2.6 pcs, which amounts to $7.8\times 10^{13}$ km. This needs to be accomplished in a human lifespan of about 80 years, which si $2.4\times 10^9$ seconds. The speed is the ratio of these numbers, or about 33,000 km/s (11% of the speed of light).

#12

The luminosity is just $5\times 10^8$ Watts in the FM band. This is 500 times bigger than the radio output of the Sun in this band!

#15

At 1 hour per star, 20,000 hours is needed, or 2.3 years. The other one requires 20,000 days, or about 55 years.