Facing the Crisis In Calculus

 

 

When it comes to calculus, we don’t get it the first time around, our colleagues don’t get it, and our students are still not getting it.  It’s no wonder that one of the most common occurrences in higher education is that of a non-mathematics faculty member discovering that something they were doing is calculus.

Something is wrong with calculus instruction, and the problem may be with the calculus curriculum itself.  Admittedly, there are ideas in calculus that will never be accessible in a first course, and this will never be corrected.   We certainly not saying that any textbook we write will cure all that is wrong with calculus.  However, there are many problems that can and should be corrected, as we point out below.  

Circular Associations

Research indicates that learning mathematics depends heavily on the ability to make connections between similar concepts.  Indeed, a particularly strong way of presenting a theorem is by placing it in the form “the following are equivalent.”  For example, in trigonometry, the association between right triangles and trigonometric functions is fundamental.

However, in the calculus curriculum, many of the associations are circular.  All too often a given concept is associated with a concept that is defined in terms of the original concept.  Such connections increase the complexity of a concept without shedding any insight on the concept itself.  Not surprisingly, concepts motivated with circular associations are the ones most often memorized with little or no comprehension. 

Consider, for example, tangent lines.  The standard approach is to use secant lines to motivate the difference quotient, after which the derivative is defined to be a limit of difference quotients.  The implication is that the derivative is the slope of the tangent line, except that the tangent line itself is never defined.  What then is a tangent line, according to the standard treatment?  It is, of course, the line through the point whose slope is the derivative.

The result is that students do not develop any intuition about what a tangent line is, and conversely, their understanding of the derivative is not aided by the consideration of tangent lines.  Instead, tangent lines become a metaphor for differentiation, important but without real meaning.  In general, circular associations often seem quite profound without actually revealing anything at all.  

To further illustrate, let me list additional examples from calculus along with some of the confusion that arises as a result.  (This list is not exhaustive.  Indeed, this is likely only a very small sample of the confusion in calculus we ourselves create).

1.      Review of Functions:  A function f is defined to be a relationship between two sets, and then y=f(x) is defined to be another way of writing the function.   However, y=f(x) as used in calculus is the equation of a curve in analytic geometry.  It is no wonder that so many of us mix geometric notions of tangent lines with numerical notions of local linear approximations of functions.

2.      Limits: Intuitive approaches to the limit are abundant with circular associations, but I want to pick on the formal definition of the limit.  Most undergraduate analysis courses begin with sequences because sequences give us a means of actually associating “x is approaching a” with “f(x)  is approaching L.”   Cauchy’s definition of the limit—i.e., the formal definition—does not define the idea of “approaching.”   However, calculus texts routinely argue that “approaching” means that there is a  d>0 very, very close to 0 that forces x to be very, very close to a, which in turn forces f(x) to get very, very close to L, so close that it is within e>0 of L  even e>0 when is itself very, very close to 0.  That is, "approaching" is defined to mean "satisfies Cauchy's definition," and then Cauchy's definition is said to imply approaching. To see why this association is circular, consider that if f(x)=L is constant, then it is within any e of L regardless of the value of x—it need not be anywhere close to a given value a, much less approaching it. 

3.      Derivatives:  Derivatives are applied to differentiable functions, where a function is differentiable at a point if its derivative exists at that point.  Differentiability as an independent concept is only briefly explored.

4.      Definite Integral:  In most calculus courses, antiderivatives are introduced  without motivation and then a few sections later, the fundamental theorem implies an association between definite integrals and antiderivatives—an association our students have assumed all along (after all, both use the same symbol).  Thus, the amazing connection between differentiation and integration is anti-climatic, at best.

5.      Applications of the Integral:  The motivation behind “applications of the integral” is to associate the definition of the integral with concepts other than area.  However, these contrived applications are outside of most mathematicians’ training, which means mathematicians must use the definite integral to define the ideas in the application itself.  For example, work becomes an integral of force, instead of the proper interpretation that work can be associated with force via an integral.  

8.      Techniques of Integration:  We learn certain techniques to evaluate integrals because there are integrals that can be evaluated with those techniques.  There are other techniques and other integrals, but those techniques are not considered because those integrals do not appear in the text.

9.      Sequences and Series; Convergence Tests: We learn convergence tests for certains types of series because there are series that can be tested with those convergence tests.  There are other series and other convergence tests, but those convergence tests are not considered because those series are not introduced in the text.

10.  Taylor’s Theorem: Taylor Series: Taylor Polynomials: Taylor, Taylor, Taylor, Taylor!  In almost any calculus text, the 2 or 3 sections on Taylor series follow section after section of unmotivated convergence tests, and in those few short sections the word Taylor is used so many times that it is no wonder that students never seem to understand what all those different Taylor things are all about.

 

Although calculus is but the tip of the analysis iceberg, many of the problems mentioned above can be fixed with nothing more than a little reorganization, the omission of a few extraneous ideas, and the expansion of a few underdeveloped topics. For example, is there not enough material and sufficient conceptual importance to warrant an entire, separate chapter on Taylor Polynomials, Taylor’s theorem, and Taylor’s Series?

 

The Mean Value Theorem

            Even when reformed textbooks include the Mean Value theorem (as well they should), they seldom include a proof of the Mean Value theorem. Traditional textbooks, on the other hand, place a great deal of emphasis on the route from extreme value theorem to Rolle's theorem to the Mean Value theorem. The extreme value theorem itself is never proven, since a proof requires the Heine-Borel theorem or its equivalent.

            Instead, we assume the extreme value theorem is obvious.  We simply tell the students that if f(x) is continuous on [a,b], then it must look like the picture shown in figure 1, thus proving that there is a c in [a,b] such that f(c) maximizes  f over [a,b]. 

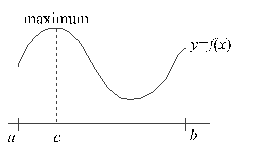
Figure 1: "Proof" of the Extreme Value Theorem

As innocent as it may seem, the assumption that all continuous functions resemble the curve in figure 1 is what prevented eighteenth century mathematicians from seeing the lack of rigor in their study of calculus.

            Graphs of continuous functions can differ radically from the curve in figure 1.  Indeed, a continuous function can have an infinite number of relative extrema over a closed interval [a,b], For instance, self-similarity implies an infinite number of relative maxima for the fractal interpolation function shown below.

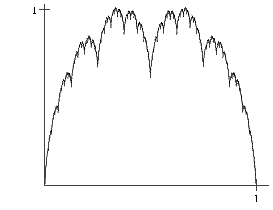
Figure 2: A Fractal Interpolation Function

 

It is not at all obvious to our students that the continuous fractal function attains the supremum of those maxima.

Thus, the extreme value theorem is far less obvious than the Mean Value theorem itself, and indeed, the fact that a continuous function attains its maximum over a closed interval is a remarkable result. Unfortunately, when our majors encounter the far from trivial proof of the extreme value theorem in an analysis course, they usually miss the point.  And it is because their traditional calculus course misleads them into thinking about continuity solely as in figure 1.

 

 

Proof by Picture

The practice of “proof by picture” is almost always flawed.  For example, the intermediate value theorem is justified with the same type of picture that is used to justify the extreme value theorem. This further reinforces the notion that “continuity means piecewise analytic with a cusp here or there.”  And this leads to “differentiability means piecewise analytic with possibly a cusp here or a vertical tangent there.”

Moreover, a “proof by picture” often gives students a fuzzy, unsophisticated view of rigor, and I would argue that Math Reasoning courses exist almost exclusively as a tool to address the flawed concepts of rigor and proof inherent in most calculus courses. As an example, consider that Newton's method is visualized but never proven.  As one of my students once said, “If you change the picture, you get a whole different method.”  That is, we rely on a picture as sole justification that Newton’s method “usually” works.  

There are many other occasions when claims of rigor are based on illustrations (derivative of the sine function, multivariable second derivative test), and in many cases, the diagrams which claim to be proofs are misleading or biased toward special cases. Can continuity of the sine and cosine functions really be inferred from the unit circle?  Diagrams and illustrations are appropriate in calculus and should be used. However, they should be as illustrations of concepts, not as proofs of theorems.

 

Infinity is not a Number

 

At the risk of beating a dead horse, let me mention one more problem with the use of pictures and diagrams.  Too often, calculus textbooks use infinity as a number, such as when they use pictures to justify writing

However, doing so immediately requires a student to exhibit a level of sophistication that many professional mathematicians seldom reach. 

In particular, infinity as a number requires the arithmetic implied by indeterminate forms.  Thus, it means that students must be able to relate a limit such as

 

to the limit calculation below which results in an indeterminate form:

The task then becomes trying to distinguish the occasional use of infinity as a number from other uses of infinity when it is not appropriate to use it as a number (such as in the sum of the limits theorem).  The individual limits above do not exist—even though we have been using infinity as a number—so that the limit of a sum theorem does not apply.  That is, infinity as a number may be too confusing for an introductory course.

Theorem Now, Proof Years Later

I have been told that calculus textbooks should be intuitive but with some rigor.  Certainly, all intuition and no rigor is a pseudo-intellectual exercise that usually results in little more than sophisticated cave drawings.  But to be completely rigorous, a calculus course would have to begin with sequences, series, and the topology of the real line, which may work against teaching the physics major to be able to think of speed as the ratio of a small change in distance ds to a small change in time dt.  

However, a theorem should be motivated even when it is not proven, and yet many theorems in calculus are stated without even the slightest suggestion as to why they are true. Error bounds in numerical integration rarely have even the slightest justification. Taylor's theorem usually descends from on high.

Indeed, textbooks often present calculus as theoretical overkill with theorems that will not be proven to our students for years to come (if at all). To illustrate, suppose a student is asked to test the following series for convergence:

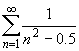
The comparison test fails because n² - 0.5< n².  Today’s calculus courses either ignore such problems or require the use of the limit comparison test, which by that point in the course is little more than another pie-in-the-sky, memorize-or-die convergence test.

            But would it not make more sense to simply re-index the series,

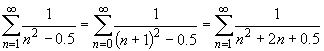
and then use the comparison test? Do we really need to introduce another unmotivated, unjustified convergence test?  Indeed, references to high-powered theorems and relatively inaccessible techniques are not nearly as necessary as traditional books would have us think.

And even when a proof is included, it is not clear why that theorem deserved proof when something else did not. We prove that the limit of a sum is the sum of the limits, but almost never is it shown that the limit of a product is the product of the limits.  We prove the sandwich theorem, we prove that differentiable at a point implies continuous at a point, we prove that derivative positive on an interval implies function increasing on that interval.

But we don’t prove the intermediate value theorem, the extreme value theorem, the chain rule, the convergence of Newton’s method, Taylor’s theorem, the ratio test, the root test, the monotone convergence theorem for sequences, and on, and on, and on. 

Where on earth does the end correction formula for Simpson’s rule come from?  Or Simpson’s rule itself, for that matter?  Is concavity defined in most Calculus courses?  Don’t we need uniform convergence in order to differentiate and integrate series?  If we are going to use conditionally convergent series, then shouldn’t we say that certain rearrangements of conditionally convergent series lead to different sums?

Calculus is not completely rigorous, nor should it be.  However, calculus courses would be better served if there was a strategy and a consistency in selecting which theorems should have proofs, which definitions should be completely rigorous, and which algorithms should be completely justified.  The fact that there is no rhyme or reason to when we do prove a theorem and when we don’t prove one is a terrible way to introduce our students to higher mathematics.  It is no wonder they enter their math reasoning and modern algebra courses with absolutely no concept of what it means to prove a theorem.

Some Perspective on Concepts

            Calculus is and should be concept-based.  However, according to Webster, a concept is nothing more than a general notion or idea.  That is, concepts are essentially a first refinement of intuition, and math based on intuition is to be avoided, as we learned the hard way 150 years ago.  Instead, mathematicians long ago realized that rigorous definitions must be used to place concepts in a mathematical setting.   Thus, mathematics, like all of the other sciences, is concept-based, but only after the concepts have been made into definitions.  

            Unfortunately, in many calculus courses, concepts are often explored without ever being rigorously defined.  The results may be entertaining, but they are not mathematical.  There simply is too much exploration which does not lead to definition.  Indeed, no meaningful theorems can be built upon or even implied by such a foundation. 

For example, a common practice is to use “zooming” to explore limits.  However, we can zoom till we drop, and yet we will not have obtained more than one or two loose conjectures about limits.  A better practice would be to zoom a few times to get a feel for what a definition of the limit should be, and then use the zooming process as motivation for a rigorous definition of the limit.  Having captured the “zooming to estimate limits” concept in a definition, we can now begin to prove theorems based on the definition, and those theorems will imply new technologies, which will in turn lead to new concepts, new explorations, and eventually, new definitions and theorems.

I think that we must be very careful when using the “rule of 3” or when incorporating technology into the curriculum.  Visualization is a powerful tool, but visualization did not take mankind from projectile motion to general relativity, nor could it.  It was the definition—theorem—proof cycle which allowed us to move from the obvious to the spectacular.  Number crunching and numerical simulations cannot be arranged into a comprehensive theory of statistics.  Instead, the numerical algorithms of statistics are implied by the theoretical results.  Thus, if the “rule of 3” is ever used to imply that the visual and the graphical are on equal terms with the analytical, then it has failed, regardless of how the students fare in the course.     

Concepts are why we study mathematics, but they are not what we study in mathematics.  Calculus courses—indeed, all mathematics courses—should emphasize that doing mathematics means definitions, theorems, proofs, and examples.   Visualization and conceptualization are useful and commendable, but they should never be the centerpieces of a mathematics course.

Summary of “Facing the Crisis”

            Thus, there is much that is wrong with calculus and a great deal of evidence that the crisis in calculus continues.   Admittedly, no course will ever be able to address all these difficulties, but that should not keep us from trying to correct as much as is possible.

             Moreover, the flaws with the calculus curriculum are further compounded by the fact that calculus has become a high school course, a community college course, and even an online course.  Indeed, the calculus curriculum is poised to confuse and befuddle on a grander scale than we have ever seen before.