A Four-Stage Model

of

Mathematical Learning

 

 

Jeff Knisley

Department of Mathematics

East Tennessee State University

Box 70663

Johnson City, TN 37614-0663

 

Phone: (423) 439-7065

Email: Knisleyj@etsu.edu

 

 

Introduction

Research in education and applied psychology has produced a number of  insights into how students think and learn, but all too often, the resulting impact on actual classroom instruction is uneven and unpredictable.  In response, many in higher education are translating research in education into models of learning specific to their own disciplines (Felder, et.al, 2000) (Buriak, McNurlen, and Harper, 1995).  These models in turn are used to reform teaching methods, to reinvent existing courses, and even to suggest new courses. 

Research in mathematics education has been no less productive, but implementation of that research often leads to difficult questions such as “how much technology is appropriate,” and “in which situations is a given teaching method most effective.”  In response, this paper combines personal observations and education research into a model of mathematical learning.  The result is in the spirit of the models mentioned above, in that it can be used to guide the development of curricular and instructional reform. 

Before presenting this model, however, let me offer this qualifier.  Good teaching begins with a genuine concern for students and an enthusiasm for the subject.  Any benefits derived from this model are in addition to that concern and enthusiasm, for I believe that nothing can ever or should ever replace the invaluable and mutually beneficial teacher-student relationship.

 

Some Results From Education Research

            This section briefly reviews the research results in mathematics education and applied psychology that most apply to this paper.  This is far from exhaustive and no effort is made to justify the conclusions in this section.  Interested readers are referred to the references for more information.

Decades of research in education suggest that students utilize individual learning styles (Felder, 1996).   Instruction should therefore be multifaceted to accommodate the variety of learning styles.  The literature in support of this assertion is vast and includes textbooks, learning style inventories, and resources for classroom implementation (e.g., Dunn and Dunn, 1993).  

Moreover, decades of research in applied psychology suggest that problem solving is best accomplished with a strategy-building approach.  Indeed, studies of individual differences in skill acquisition that suggest that the fastest learners are those who develop strategies for concept formation (Eyring, Johnson, and Francis, 1993).  Thus, any model of mathematical learning must include strategy building as a learning style.

            As a result, I believe that the learning model most applicable to mathematics is Kolb’s learning model (see Evans, et al., 1998, for a discussion of Kolb’s model).  In the Kolb model, a student’s learning style is determined by two factors—whether the student prefers the concrete to the abstract, and whether the student prefers active experimentation to reflective observation.  This results in 4 types of learners:

·        Concrete, reflective:  Those who build on previous experience.

·        Concrete, active: Those who learn by trial and error. 

·        Abstract, reflective:  Those who learn from detailed explanations. 

·        Abstract, active: Those who learn by developing individual strategies

 

Although other models also apply to mathematics, there is evidence that differentiating into learning styles may be more important than the individual style descriptions themselves (Felder, 1996).

Finally, let us label and describe the undesirable “memorize and regurgitate” method of learning.  Heuristic reasoning is a thought process in which a set of patterns and their associated actions are memorized, so that when a new concept is introduced, the closest pattern determines the action taken (Pearl, 1984).  Unfortunately, the criteria used to determine closeness are often inappropriate and frequently lead to incorrect results. 

For example, if a student incorrectly reduces the expression

to the expression x2+2x, then that student likely used visual criteria to determine that the closest pattern was the root of a given power.  That is, heuristic reasoning is knowledge without understanding, a short circuit in learning that often prevents critical thinking.  Moreover, such an arbitrary and unreliable approach to problem solving must surely be responsible for much of the “math anxiety” that so often plagues students in introductory courses.

Kolb Learning in a Mathematical Context

            The model in this paper is based on the idea that Kolb’s learning styles translate directly into mathematical learning styles.  For example, “concrete, reflective” learners are those who use previous knowledge to construct allegories of new ideas.[1]  In mathematics courses, these are the students who approach problems by trying to mimic an example in the textbook.  In similar fashion, the other three Kolb learning styles also translate into mathematical learning styles:

 

Moreover, several years of observation, experimentation, and student interaction suggest to me that these are the only four learning styles, although certainly more research into this assertion is warranted.

For example, in one experiment, I made sure that each student knew the Pythagorean theorem and had a ruler.  I then asked them to find the length of the hypotenuse of a right triangle with sides of length 2¼” and 3”, respectively.

 

 

 

 


Figure 1: Right Triangle with Unknown Hypotenuse

Some students flipped through the textbook looking for a similar example, many measured the hypotenuse with their ruler, some used the Pythagorean theorem directly, and a handful realized that the triangle is a 3-4-5 triangle (in units of ¼). 

However, there were no other styles utilized, and similarly, in other experiments I have conducted, only a bare handful of students have ever utilized styles other than the four mentioned above.  In addition, I have observed that the learning style of a given student varies from topic to topic, and unfortunately that when a student’s learning style is not successful, that student will almost always resort to heuristic reasoning. 

Four Stages of Mathematical Learning

            Thus, the question becomes, “What leads a student to choose a given style when presented with a new concept?”  I have concluded that variations in learning style are often due to how successful a student has been in translating a new idea into a well-understood concept.  Indeed, it appears that each of us acquires a new concept by progressing through 4 distinct stages of understanding:

 

It then follows that the learning style of a student is a measure of how far she has progressed through the 4 stages described above:

 

It also follows that a student’s learning style can vary, although in practice a student’s style tends to remain constant over a range of similar concepts.  

The Importance of Allegories

 

This model suggests that learning a new concept begins with allegory development.  That is, learning begins with a figurative description of a new concept in a familiar context.  Moreover, the failure to allegorize leads to a heuristic approach.  That is, if a student has no allegorical description of a concept, then he will likely resort to a “memorize and associate” style of learning. 

            Consider, for example, teaching the game of chess without the use of allegories.  We would begin by presenting an 8 by 8 grid in which players 1 and 2 receive tokens labeled A, B, C, D, E, and F arranged as shown in figure 2.  

 

 

 

 

 

 

 

 


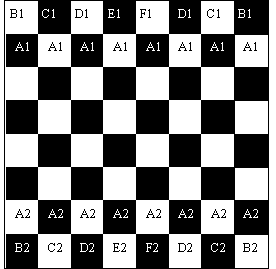
Figure 2: Chess without Allegories

We would then explain that valid moves for a token are determined by the token’s type and that the goal of the game is to immobilize the other player’s “F” token.  In response, students would likely memorize valid moves for each token and would use visual cues to motivate token movement—i.e., not much fun.

            Clearly, learning requires allegory development.  Indeed, people learn and enjoy chess because the game pieces themselves are allegories within the context of medieval military figures.  For example, pawns are numerous but have limited abilities, knights can “leap over objects,” and queens have unlimited power.  Capturing the king is the allegory for winning the game.   In fact, a vast array of video and board games owe their popularity to their allegories of real-life people, places, and events. 

In my own teaching, I have found that arithmetic is one of the most useful and most enjoyable contexts for allegories in mathematics.  For example, many of us already use the multiplication of integers, such as in

to motivate the fact that abac=ab+c.  In addition, visual and physical models also serve as appropriate contexts for allegories as long as they are easily understood and presented in a familiar fashion. 

Components of Integration

            Once a new concept has been introduced allegorically, it must be integrated into the existing knowledge base.  I believe that this process of integration begins with a definition, since a definition assigns a label to a new concept and places it within a mathematical setting.  Once defined, the concept can be compared and contrasted with known concepts.   

            Visualization, experimentation, and exploration play key roles in integration.  Indeed, visual comparisons are the most powerful, and explorations and experiments are ways of comparing new phenomena to well-studied, well-understood phenomena.  As a result, the use of technology is often desirable at this point as a visualization tool.

            For example, once exponential growth has been allegorized and defined, students may best be served by comparisons of the new phenomenon of exponential growth to the known phenomenon of linear growth.  Indeed, suppose that students are told that there are two options for receiving a monetary prize—either $1000 a month for 60 months or the total that results from an investment of $100 at 20% interest each month for 60 months.  The visual comparison of these options reveals the differences and similarities between exponential and linear growth (see figure 3 below).  In particular, exponential growth appears to be almost linear to begin with, and thus for the first few months option 1 will have a greater value.  However, as time passes, the exponential overtakes and grows increasingly faster than the linear option, so that after 60 months, option 1 is worth $60,000 while option 2 is worth $4,695,626.

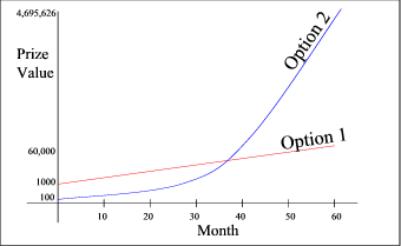
Figure 3:  Visual Comparison of Linear and Exponential Growth

 

Analysis and Synthesis

            In short, analysis means that the student is thinking critically about the new concept.  That is, the new concept takes on its own character, and the student’s desire is to learn as much as possible about that character.  Analyzers want to know the history of the concept, the techniques for using it, and the explanations of its different attributes.  Moreover, the new concept also becomes one of many characters, so that analyzers also want to know connections to existing concepts as well as the sphere of influence of the new concept within their existing knowledge base. 

As a result, analyzers desire a great deal of information in a short period of time, and thus, it is entirely appropriate to lecture to a group of analyzers.  Unfortunately, the current situation is one in which we assume that all of our students are analyzers for every concept, which means that we deliver massive amounts of information to students who have not even realized that they are encountering a new idea.  This, in fact, appears to be the case for the limit concept in calculus.  Studies have shown that almost no one completes a calculus course with any meaningful understanding of limits (Szydlik, 2000).  Instead, most students resort to heuristics to survive the initial exposure to the limit process.

Finally, synthesis is essentially mastery of the topic, in that the new concept becomes a tool the student can use to develop individual strategies for solving problems.  For example, even though games often depend heavily on allegories, the fun part of a game is analyzing it and developing new strategies for winning.  Indeed, all of us would like to reach the point in any game where we are in control—that is, the point where we are synthesizing our own strategies and then using those strategies to develop our own allegories of new concepts. 

The Role of the Teacher

            As mentioned in the introduction, the value of this 4-stage model of mathematical learning is that it can be used as a guide to implementing reform methods and curriculum.   For example, we can use this model to describe and explore the role of the teacher in a reformed mathematics course. 

To begin with, synthesis is a creative act, and thus, not all students will be able to synthesize with a given concept.  Moreover, appropriate allegories are based on a student’s cultural background, and as a result, new allegories must be developed continually.  Finally, some concepts require more allegorization, integration, and analysis than others.  Simply put, this model does not allow us to reduce mathematical learning to an automated process with 4 regimented steps. 

            As a result, there must be an intermediary—i.e., a teacher—who develops allegories for the students, who determines how much allegorization, integration, and analysis should be used in presenting a concept, and who insures that students learn to think critically about each concept.  And once students can think critically, the teacher will need to synthesize for many of the students by presenting problem-solving strategies and creating new allegories.

            To be more specific, this model suggests the following roles for the teacher in each of the 4 stages of concept acquisition:  

 

Space does not permit me to elaborate on each role, but let me point out one that I feel should not be neglected.  Students who have talent are too often bored or even stifled in our educational system.  If we accept that a coach is someone who applies discipline and structure to creativity, then clearly these are students who need to be coached.  In particular, teachers need to insure that synthesizers realize that there is creativity in mathematics, and they need to show that such creativity is both enjoyable and rewarding. 

The Role of Technology

            Although reform ideas such as the use of technology, group learning, and the rule of 4 are valuable and effective, their implementation often requires a great expenditure of valuable class time.  If not used wisely, reform ideas can easily lead to courses which have depth but no breadth, which is entirely inappropriate for a college-level curriculum.

            However, the 4-stage model of learning allows us to develop a strategy for implementing reform that leads to little, if any, sacrifice of course content.  To illustrate this assertion, I will limit my comments to the incorporation of technology into the curriculum. 

            Suppose that we have a concept that lends itself to the use of technology.  To determine how best to utilize that technology, we need to first determine which of the four stages best describes that technology, and then we need to restrict our use of that technology to that stage of the presentation of that concept.  Moreover, if we determine that students generally need very little time in that stage, then we may not want to use that technology at all.

            For example, suppose we have an “applet” that demonstrates the convergence of Riemann sums to the area under a curve.  There is no comparison of known ideas to unknown ideas, nor does this applet aid in distinguishing the concept of the integral from any other concept (such as the concept of the antiderivative).  Thus, it is not appropriate (in my opinion) for integration, analysis, or synthesis. 

However, if the applet is simple to understand and easy to use, then it should serve as an excellent visual context for introducing the concept of the integral.  Thus, I would use the applet as an allegory for the definite integral.  I would introduce it as an illustration of the next concept we want to consider, and then I would use it to motivate the definitions of partition, Riemann Sum, and ultimately, the definite integral.  

In fact, I might decide that a couple of well-drawn pictures are just as effective as the applet, and thus, I might feel justified in avoiding the time and effort needed to present the applet and describe how it is used.  Or I might decide that I really want to use the applet, and consequently, I might design an assignment that asks them to compare applet results to results produced with pencil and paper.

Moreover, my usage will vary from semester to semester.  In a given semester I may decide that individual and class needs dictate that I spend more time allegorizing the definite integral concept than I did in another semester.  Or I may present the applet simply as an opportunity to challenge a group of synthesizers to produce a better applet with the promise that I will use their in place of the one presented. 

Regardless, my usage or non-usage of the technology is guided by the model’s identification of what role that technology can play in presenting a certain concept.  It is amazing to me how much initially impressive technology actually has very little instructional value with respect to this model.    

Conclusion   

            Finally, I want to re-iterate my belief that the model is effective only as a tool in the hands of an enthusiastic teacher who wants to enhance the student-teacher relationship.  In fact, I suspect that many teachers use this model already, although they have not formalized it.  Many of us already measure a hypotenuse with a ruler in order to corroborate the use of the Pythagorean theorem, and we do so because we know that once the student sees that the measurements and the theorems produce the same results, they will use the theorem independent of any measurements.

            Nonetheless, this model has become an invaluable tool in my teaching.  It allows me to diagnose student needs quickly and effectively, it helps me budget my time and my use of technology, and it increases my students’ confidence in my ability to lead them to success in the course.  I hope it will be of equal value to my fellow educators in the mathematics profession.

References

Bloom, B. S. Taxonomy of Educational Objectives.  David McKay Company. New York. 1956.

Buriak, Philip, Brian McNurlen, and Joe Harper. “System Model for Learning.” In Proceedings of the ASEE/IEEE Frontiers in Education Conference 2a (1995).

Dunn, R.S., and Dunn, K.J.  Teaching Secondary Students Through Their Individual Learning Styles:  Practical Approaches for Grades 7-12.  Allyn & Bacon, 1993. 

Evans, Nancy J., Deanna S. Forney, and Florence Guido-DiBrito. Student Development in College:  Theory, Research, and Practice.  Jossey-Bass. 1998.  

Eyring, James D., Debra Steele Johnson, and David J. Francis. “A Cross-Level Units of Analysis Approach to Individual Differences in Skill Acquisition.” Journal of Applied Psychology 78(5) (May 1993): 805 – 814.

Felder, Richard M.  “Matters of Style.” ASEE Prism 6(4) (December 1996):18-23.

Felder, Richard M., Donald R. Woods, James E. Stice, and Armando Rugarcia.  “The Future of Engineering Education:  II. Teaching Methods that Work.” Chem. Engr. Education.  34(1) (January, 2000): 26-39.

Lee, Frank J., John R. Anderson, and Michael P. Matessa. “Components of Dynamic Skill Acquisition.”  In Proceedings of the Seventeenth Annual Conference of the Cognitive Science Society (1995): 506-511.

Pearl, J.  Heuristics: Intelligent Search Strategies for Computer Problem-Solving. Addison-Wesley, Reading, MA, 1984.

Szydlik, Jennifer Earles.  “Mathematical Beliefs and Conceptual Understanding of the Limit of a Function.” Journal for Research in Mathematics Education 31(3) (March 2000): 258-276.


[1] An allegory is a figurative description of an unknown idea in a familiar context.