Three dimensional space, which is also denoted R3 (pronounced (are-3)), has an additional axis known as the z-axis. In particular, we draw the z-axis as a vertical line which intersects a "horizontal'' xy-plane at the origin.

We say that the coordinate system is right-handed because if the fingers of the right hand are wrapped about the z-axis in the counter-clockwise direction, then the thumb of the right hand points in the positive z-direction.
A point P1(x1,y1,z1) in R3 is the point that has a vertical displacement of z1 above the point (x1,y1,0) . Points in the xy-plane are thus of the form (x1,y1,0) , which we often simply write as (x1,y1) .
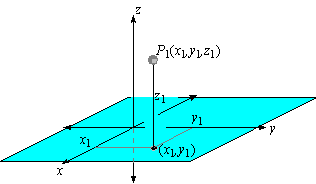
That is, if a point is in the xy-plane, then we will continue to write it with only two coordinates.
Given points P1( x1,y1,z1) and P2(x2,y2,z2) in R3, we define the vector between them to be
| (2) |
EXAMPLE 3 Find the vector with initial point P1(4,3,5) and terminal point P2( 3,6,4) .
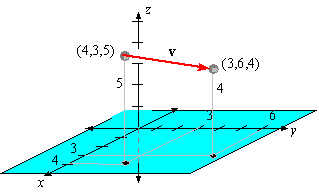
Solution: To do so, we use (2) to obtain
v = á 3-4,6-3,4-5 ñ = á-1,3,-1 ñ
Moreover, to aid in visualization, this text will include many figures which are interactive. These figures are prepared using the computer algebra system Maple along with the packages Javaview and LiveGraphics3D.
For example, the figure below is a vector with initial point (4,1,2) and terminal point (1,6,5).
If you "click and drag" on the figure, it will rotate. Right-clicking allows you to select scaling and rotation as well. Although not labeled, these figures will be easily distinguished by their unique appearance.