Part 4: Position Vectors and Equations of Lines
If a vector P is fixed at the origin and if it
terminates at P( x,y,z), then P
is a position vector for a point P(x,y,z) . As a result, each point in
R3
corresponds to a 3-dimensional position vector.
Correspondingly, if P =
áx,y,z
ñ is a position vector, then it corresponds
to a point P( x,y,z) .
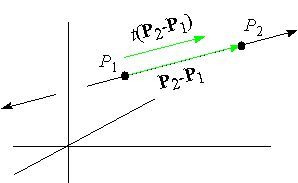
Suppose that t is a scalar (i.e., a number) and that P1(x1,y1,z1) and P2( x2,y2,z2) are
distinct points. Then the vector t( P2-P1) is parallel to the line through P1 and P2.
If L( t) denotes the sum of P1 and t( P2-P1) , then L( t)
defines a position vector-i.e., a point-on the line through P1 and P2.
Since P1+t( P2-P1) = (1-t) P1+tP2, this means that the set of all
points L( t) on the line through P1
and P2 are given by the formula
with L( 0) = P1 and L(1) = P2. Substituting P1(x1,y1,z1) and P2( x2,y2,z2) leads
to
|
L( t) =
á ( 1-t)x1+tx2,( 1-t) y1+ty2,( 1-t)z1+tz2
ñ |
| (4) |
Switching the roles of P1 and P2 is equivalent
to interchanging ( 1-t) and t in the definition of L(t) .
EXAMPLE 6 Find the equation of the line which passes through
the points P1( 1,0,1) and P2( 4,3,2) .
Solution: The formula (3) reduces to
|
L( t) = ( 1-t) P1+tP2 = ( 1-t)
á 1,0,1
ñ +t
á4,3,2
ñ |
|
Vector arithmetic or equivalently, (4), leads to
|
L( t) =
á 1-t+4t,0+3t,1-t+2t
ñ =
á 3t+1,3t,t+1
ñ |
|
That is, L( t) =
á 3t+1,3t,t+1
ñ .
For example, when t = 2, we obtain the position vector L(2) =
á 3·2+1,3·2,2+1
ñ =
á7,6,3
ñ , which yields the point P3( 7,6,3) . Likewise, when t = -1, we obtain the position vector L(-1) =
á -2,-3,0
ñ , which corresponds to the
point P0( -2,-3,0) .
Equations (3) and (4) are known
as parametric representations of a line. There are other
representations as well, but we restrict our attention to the parametric
representations in this text because of their utility.
For example, parameteric representations can be used to determine if two
lines intersect. If L( t) and K(s) are the equations of the two lines, respectively, then equating
their components leads to 3 equations in the 2 unknowns s and t. If a
solution exists, then the two lines intersect. Otherwise, they do not.
EXAMPLE 7 Find the equation of the line through P1(0,1,3) and P2(
2,0,6) . Then find the equation of
the line through P3( -1,1,1) and P4( 2,2,-2) and determine if the two lines intersect.
Solution: The line through P1( 0,1,3) and P2( 2,0,6) is
|
L( t) = ( 1-t)
á 0,1,3
ñ+t
á 2,0,6
ñ =
á 2t,1-t,3t+3
ñ |
|
while the line through P3( -1,1,1) and P4(2,2,-2) is
|
K( s) = ( 1-s)
á-1,1,1
ñ +s
á 2,2,-2
ñ =
á3s-1,s+1,-3s+1
ñ |
|
The lines intersect when L( t) = K(s) , which is
when
|
3s-1 |
= |
2t, |
|
s+1 |
= |
1-t, |
|
-3s+1 |
= |
3t+3 |
| 1.5s-0.5 |
= |
t |
|
s |
= |
-t |
|
s |
= |
-t-2/3 |
|
Combining the first two equations leads to
Thus, s = -t implies that s = 0.2. However, substituting into the last
equation s
= -t-2/3 leads to
|
0.2 = 0.2-2/3 or 0 = -2/3 |
|
Since s = 0.2 and t = -0.2 are not solutions to the last equation, the 3
equations together have no solution. Thus, the lines do not intersect.