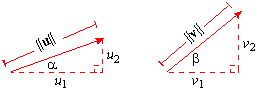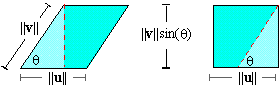Part 2: Area of a Parallelogram

In the last section, we saw that the 2 dimensional vectors u = á u₁,u₂,0 ñ and v = á v₁,v₂,0 ñ can be written in polar form as

u = á || u|| cos( a) ,|| u|| sin( a),0 ñ v = á || v|| cos( b) ,|| v|| sin( b),0 ñ

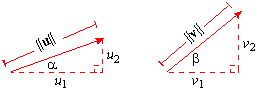Let's compute u×v in polar form using the formula (4):

u×v = 0,0, || u|| cos( a) || u|| sin( a) || v|| cos( b) || v|| sin( b) = á 0,0,|| u|| cos( a)|| v|| sin( b) -|| v|| cos( b) || u|| sin(a) ñ = á 0,0,|| u|| || v||[ sin( b) cos( a) -sin(a) cos( b) ] ñ

Simplifying with the difference of two angles formula for the sine function yields

u×v = á 0,0,|| u|| || v|| sin( b-a) ñ

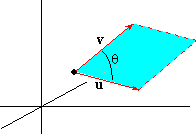
However, the angle q between u and v is related to b and a by q = | b-a| . In fact, the following can be shown:      

Theorem 3.3: If q is the angle formed by u and v, then

|| u×v|| = || u|| || v|| sin( q)

       

Moreover, since a parallelogram can be cut into two parts which form a rectangle with height || v|| sin( q) and base || u|| ,

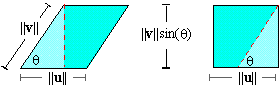
the area of the parallelogram formed by u and v is || u|| || v|| sin( q) . Thus, theorem 3.3 implies that

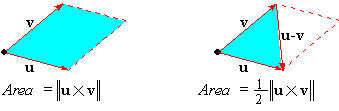
The latter result follows from the fact that u-v bisects the parallelogram formed by u and v.

       

EXAMPLE 3    Find the area of the triangle with vertices at P₁( 2,2) , P₂( 4,4) , and P₃(6,1) .

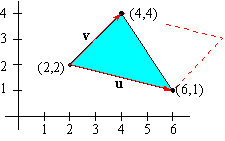
Solution: It is easy to see that u = á2,2 ñ and v = á 4,-1 ñ . As vectors in R³, we have u = á2,2,0 ñ and v = á 4,-1,0 ñ . Thus, their cross product is

u×v = 2 0 4 0 , 0 2 0 -1 , 2 2 4 -1 = á 0,0,  2·( -1) -4·2   ñ = á 0,0,-10 ñ

Since the triangle has half of the area of the parallelogram formed by u and v, the area of the triangle is

Area = || u×v|| =   1 2 02+02+(-10) 2   = 5  units2

       

EXAMPLE 4    Find the area of the triangle with vertices P₁( 3,0,2) , P₂( 4,6,1) , and P₃(0,5,4) .

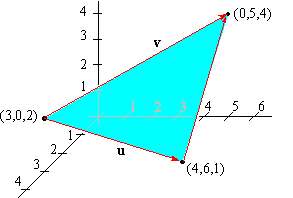
Solution: To do so, we first construct the vectors u and v:

u  =   P1P2   = á4-3,6-0,1-2 ñ = á 1,6,-1 ñ v  =  P1P3   = á0-3,5-0,4-2 ñ = á -3,5,2 ñ

As vectors in R³, we now have u = á2,2,0 ñ and v = á 4,-1,0 ñ . Thus, their cross product is

u×v = 6 -1 5 2 , -1 1 2 -3 , 1 6 -3 5 = á 6·2-5·( -1) ,( -1) ·( -3) -2·1,1·5-( -3) ·6 ñ = á 17,1,23 ñ

Since the triangle has half of the area of the parallelogram formed by u and v, the area of the triangle is

Area = || u×v|| =   1 2 172+22+232   = 14.335  units2

Maple/Javaview Figure