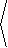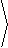Part 3: Orthogonality

Let's use the definition to calculate u·( u×v) when u = áu₁,u₂,u₃ ñ and v = áv₁,v₂,v₃ ñ : 

u · ( u×v ) = u1 u2 u3 v2 v3  + u2  u3 u1 v3 v1  + u3 u1 u2 v1 v2 =  u1(u2 v3 - v2 u3) + u2(u3 v1 - v3 u1) + u3(u1 v2 - v1 u2)  = u1 u2 v3 - u1 u3 v2 + u2 u3 v1 - u2 u1v3  + u1 u3 v2 -  u2 u3 v1

The coloration in the last line shows that all terms cancel, so that u · ( u×v) = 0.  Since v·( u×v) = -v · ( v×u), the same calculation shows that that u×v is orthogonal to v. We summarize this result in the following theorem.       

Theorem 3.4: The cross product u×v is orthogonal to u and v.

      

As we will see in the next section and throughout the text, this property of the cross product is extremely important in many applications.

EXAMPLE 5    Show that u×v is orthogonal to u when u = á 2,3,7 ñ and v = á 1,4,2 ñ .       

Solution: To begin with, let us notice that

u×v = 3 7 4 2 ,   7 2 2 1 ,   2 3 1 4 = á 6-28, 7-4, 8-3 ñ = á -22, 3, 5 ñ

Now let's compute u·( u×v) :

u·( u×v) = á2,3,7 ñ · á -22,3,5 ñ = -44+9+35 = 0

and u, v, and u×v are shown below:

Maple/javaview image

Suppose that u is orthogonal to a unit vector n and that u_^, pronounced "u perp," is the rotation of u through an angle of 90^° about an axis parallel to n.

Maple/javaview image

Theorems 3.3 and 3.4 imply that 

u^ = n×u

That is, u_^ and u have the same length because n is a unit vector perpendicular to u, and u_^ and u are orthogonal because of theorem 3.4.

       

EXAMPLE 6    What is the vector u_^ obtained by rotating u = á a,b ñ through an angle of 90^° about the z-axis.       

Solution: The unit vector in the z-direction is k = á 0,0,1 ñ .  Thus

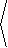
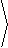
u^ = á 0,0,1 ñ × áa,b,0 ñ = 0 1 b 0 ,   1 0 0 a ,   0 0 a b = á -b,a,0 ñ

That is, u_^ = á -b,a ñ , which matches a "trick" we obtained a different way in the last section.

Maple/javaview image