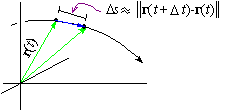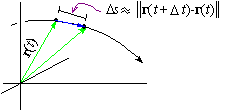Part 1: Speed

Many of us are familiar with the idea that if an object is moving in a straight line at a constant rate, then ``distance = rate × time,'' where ``rate'' is another word for speed. However, if an object is not moving in a straight line at a constant rate, then we must use calculus to define the notion of speed.

To begin with, if r( t) denotes the position of an object at time t and if Ds represents the distance the object travels along a curve over a short time period Dt, then Ds » || r( t+Dt) -r(t) || .

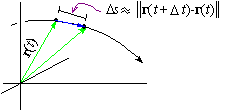
If r(t) is differentiable at each point, then the object is arbitrarily close to moving in a straight line with a constant speed from time t to time t+Dt when Dt is sufficiently small.  That is, over the short period of time from t to time t+Dt, the distance Ds and time Dt satisfy

EXAMPLE 1    Find the speed of an object with position r( t) = á t³,t²,3t ñ in feet at time t in seconds.       

Solution: Since the velocity is v( t) = á 3t²,2t,3 ñ , the speed is

ds dt  = || v|| =  9t4+4t2+9

       

The expression for the speed does not simplify any further. However, for pedagogical purposes (i.e., teaching and learning), we will see many problems in which either algebra or trigonometry can be used to reduce the expression under the radical to a perfect square.   

EXAMPLE 2    Find the speed of the object with position r( t) = á 3sin( 2t) ,5cos(2t) ,4sin( 2t) ñ in feet at time t in seconds.       

Solution: To do so, we first compute the velocity:

v = á 6cos( 2t) ,-10sin( 2t),8cos( 2t) ñ

The speed is then the magnitude of the velocity:

ds dt  =  [ 6cos( 2t) ] 2+[-10sin( 2t) ] 2+[ 8cos( 2t) ]2  =  36cos2( 2t) +100sin2( 2t) +64cos2( 2t)  =  100cos2( 2t) +100sin2( 2t)  =  10 feet per second