Part 2: The Unit Tangent Vector

As we have seen already, vectors are often represented in a bold typeface. In addition, the magnitude of a vector is often denoted by the same letter, only in an italic typeface. Thus, we often use r in place of || r|| , and likewise, we often write

v = || v( t) ||

to denote the speed of an object. Given this new notation, we define the unit tangent vector T( t) to be the unit vector in the direction of v:

T = 1 v  v

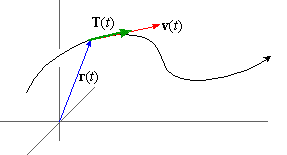
As a result, v = vT, which shows that velocity can be written as the product of its speed and direction:       

EXAMPLE 3    Find the unit tangent vector to r(t) = á e^t, 2t, 2e^-t ñ .      

Solution: To do so, we first compute the velocity:

v( t) =  d dt áet,2t,2e-t ñ = á et,2,-2e-t ñ

Then we find the magnitude of the velocity

|| v|| =    ( et)2+( 2)2+( -2e-t)2   =    (et)2 +4+4(e-t)2

Notice now that since e^te^-t = 1, the quantity under the square root can be factored into a perfect square:

|| v|| =  ( et+2e-t)2  = et+2e-t

We then divide the velocity by the magnitude to obtain the unit tangent vector:

T( t) = 1 et+2e-t v =   et et+2e-t ,  2 et+2e-t ,  -2e-t et+2e-t