Part 1: The Normal Vector
In the last section, we explored those ideas related to velocity-namely,
distance, speed, and the unit tangent vector. In this section, we do the
same for acceleration by exploring the concepts of linear acceleration,
curvature, and the normal vector.
To begin with, the velocity of a parametrization r( t)
can be written as v = vT where v is the speed and T is the unit tangent vector. As a result, the acceleration for
the curve is
Moreover, the unit tangent T satisfies || T( t) || = 1, which implies that T(t) ·T( t) = 1. Differentiation yields
|
|
( T( t) ·T( t)) |
= |
|
1 |
|
|
= |
0 |
|
|
= |
0 |
|
That is, the derivative of T is orthogonal to T, so
that (1) implies that the acceleration a is
actually the sum of two orthogonal vectors. Moreover, if we let
then N is a unit vector which is orthogonal to T and
which is thus known as the unit normal to the curve.

EXAMPLE 1 Find the unit normal N to the helix
r( t) =
á 4cos( t), 4sin(t) ,3t
ñ
Solution: Since the velocity is v =
á -4sin( t) ,4cos( t) ,3
ñ , the speed is
|
v = |
 |
|
|
16sin2( t) +16cos2( t)
+9 |
|
|
= |
|
= 5 |
|
and consequently the unit tangent vector is
|
T = |
|
v = | 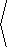 |
|
sin(t) , |
|
cos( t) , |
|
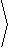
|
|
The derivative of the unit tangent vector is
|
|
= |
|
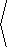
|
|
sin(t) , |
|
cos( t) , |
| 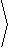 |
= | 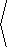 |
|
cos( t) , |
|
sin(t) ,0 |
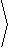
|
|
which has a length of
Thus, the unit normal is
|
N = |
|
|
= |
| 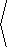 |
|
cos( t) , |
|
sin( t) ,0 |
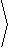
|
|
which simplifies to N =
á -cos( t) ,-sin( t) ,0
ñ . For example, if t=p
/2, then N =
á 0 ,-1 ,0
ñ , as is shown below along with the unit tangent T at
the same point.
Check your Reading: Is N the only unit vector
orthogonal to T at a given point on the curve?