Part 2: Curvature in the Plane

If r( t) is the parametrization of a 2-dimensional curve, then its velocity can be written in polar form as
v = á vcos( q) ,vsin( q) ñ

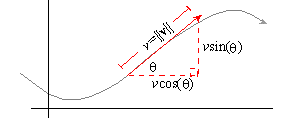
Factoring out the v then leads to v = v  á cos(q) ,sin( q) ñ , which reveals that the unit vector is

T = á cos[ q( t) ] ,sin[ q( t) ] ñ
As a result, the derivative of T is given by
dT
dt
 = 
d
dt
cos[ q(t) ]  ,
d
dt
sin[ q( t) ]
 = 
-sin[ q( t) ]
dq
dt
,cos[ q( t) ]
dq
dt
 = 
dq
dt
á -sin( q) ,cos(q) ñ

Since á -sin( q) ,cos( q) ñ is also a unit vector, the magnitude of dT/dt is

dT
dt
 = 
dq
dt
(3)
which via the chain rule is equivalent to
dT
dt
 = 
dq
ds
ds
dt
(4)
We define dq/ds to be the curvature k of the curve. That is,
k =
dq
ds
Since v = ds/dt, solving for dq/ds in (4) yields the formula
k = 
1
v
dT
dt
(5)

       

EXAMPLE 2    Find the curvature k of the curve r( t) = á t,ln| sec( t) | ñ       

Solution: The velocity is v = á 1,tan(t) ñ , so that the speed is
v =
1+tan2( t)
 = 
sec2( t)
= sec( t)
and consequently, the unit tangent vector is
T =
1
 sec( t)
á 1,tan(t) ñ = á cos( t) ,sin(t) ñ
and the derivative of the unit tangent is
dT
dt
= á -sin( t) ,cos(t) ñ
As a result, (5) implies that the curvature is
k = 
1
v
dT
dt
 = 
1
sec(t)
sin2( t) +cos2( t)
 = cos( t)

       

To better understand the concept of curvature, let us suppose that N is normal to a curve at a point P and suppose that we draw a circle with center on the line through N which passes through P and Q where Q is another point on the curve.

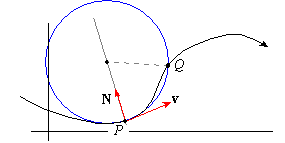
If we let Q get closer and closer to P, the result will be a sequence of circles which converge to a circle of radius R called the osculating circle at point P.

The osculating circle is practically the same as a small section of the curve, so that if we let Dq denote the change in angle between the velocity vectors v( t) and v(t+Dt) for Dt small, then elementary geometry implies that Dq is also the angle of the sector between r( t) and r( t+Dt) .

Thus, if Ds denotes the length of the arc of that sector, then Ds = RDq, which implies that

Dq
Ds
 =  
1
R
so that in the limit as Ds approaches 0, the ratio Dq/Ds approaches the curvature k. As a result, it follows that the curvature is given by
k =  
dq
ds
 =  
1
R
That is, the curvature k( t) is the reciprocal of the radius of the osculating circle.

As a result, the curvature of a circle is constant, and indeed,
k =
1
radius of the circle
Likewise, it follows that the curvature of a straight line is k = 0.       

EXAMPLE 3    Find the curvature of the circle of radius 3 parametrized by
r( t) = á 3cos( t) ,3sin(t) ñ
Solution: Since the velocity is v( t) = á -3sin( t) ,3cos( t) ñ , the speed is
v = 
9sin2( t) +9cos2( t)
 = 3
As a result, the unit tangent vector is
T( t) = á -sin( t) ,cos(t) ñ
from which it follows that
dT
dt
 = á -cos( t) ,-sin(t) ñ
As a result, the curvature is
k =  
1
v
dT
dt
 =  
1
3
cos2( t) +sin2( t)
 = 
1
3

       

Check your Reading: How is the curvature in example 3 related to the radius of the circle?