Part2: Linearization and Tangent Planes
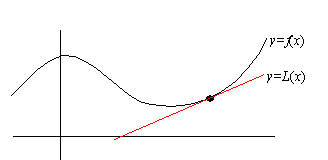
In single variable calculus, we learned that if f( x)
is differentiable at a point p, then
|
L( x) = f( p) +f'( p) (x-p) |
|
is the linearization of f( x) at x = p. Moreover, the
graph of L( x) is the straight line that is tangent to the
graph of f( x) at x = p.
Analogously, let us define the linearization of a function f(x,y) at a point ( p,q) to be
|
L( x,y) = f( p,q) +fx( p,q) (x-p) +fy( p,q) ( y-q) |
|
It follows from definition 4.1 that if f( x,y) is
differentiable at ( p,q) , then f( x,y) » L( x,y) for all ( x,y) which are sufficiently
close to a point ( p,q) . Moreover, it also follows that the
graph of L( x,y) is a plane that practically the same as the
surface z = f( x,y) near the point ( p,q,f(p,q) ) .
Thus, we say that the graph of L( x,y) is the tangent
plane to z = f( x,y) at ( p,q) .
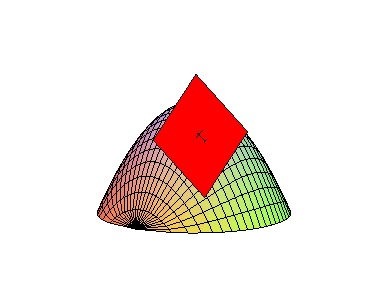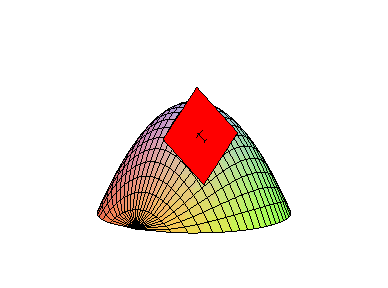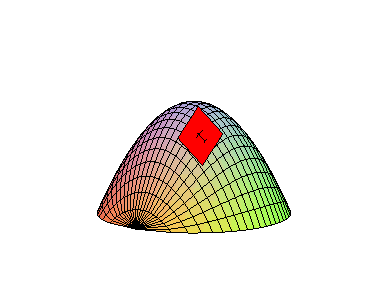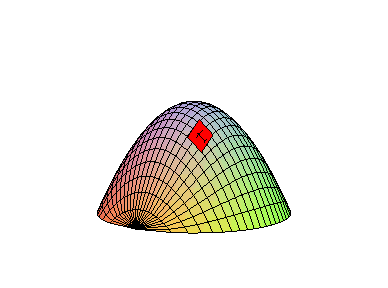
EXAMPLE 2 Find the tangent plane to f( x,y) = 9-x2-y2 when ( x,y) = ( 1,1) .
Solution: To begin with, fx( x,y) = -2x and fy( x,y) = -2y, so that fx( 1,1) = fy(1,1) = -2 and
|
|
|
|
f( 1,1) +fx( 1,1) (x-1) +fy( 1,1) ( y-1) |
| |
|
|
|
which simplifies to L( x,y) = 11-2x-2y. Thus, the equation of
the tangent plane to f( x,y) at the point ( 1,1,7) is
which is shown below.
The tangent plane is the plane that ''best approximates'' a
surface in the neighborhood of a point. However, a tangent plane may
intersect a surface in an infinite number of points. Thus, intuitive ''working definitions'' of tangency
are not tenable for functions of 2 variables, as illustrated in example 3.
EXAMPLE 3 Find the linearization of f( x,y) = x3-xy2 at the point ( 1,2) .
Solution: Since fx = 3x2-y2 and fy = -2xy, we have
|
fx( 1,2) = 3-4 = -1, fy( 1,2) = -2·1·2 = -4 |
|
Since f( 1,2) = -3, the linearization of f( x,y) =x3-xy2 at ( 1,2) is
|
L( x,y) = -3-1( x-1) -4( y-2) |
|
which simplifies to L( x,y) = 6-x-4y. The graph of L(x,y) is shown versus the graph of f( x,y) below:
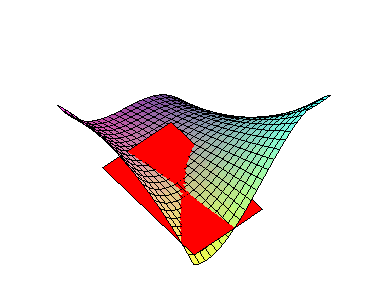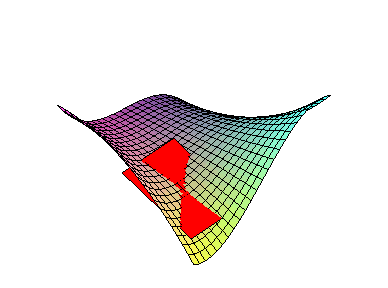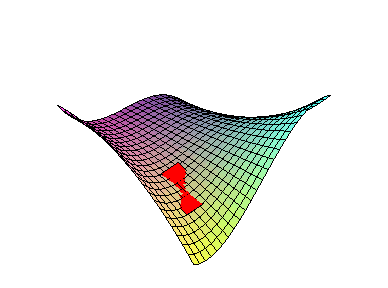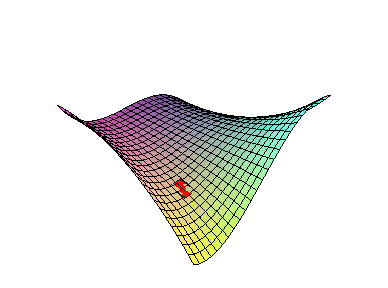
Check your Reading: How is the tangent plane to the
surface related to the surface itself?