Critical Points

In this section, we develop a method for finding the extrema-i.e.e, the maximum and minimum points-of a function of two variables. For reasons which will soon be apparent, this method is called the second derivative test.

To begin with, we say that a function f( x,y) has a local maximum at a point ( p,q) if there is a circle centered at ( p,q) such that

f( x,y) £ f( p,q)

for all ( x,y) in that circle. That is, f( p,q) is the maximum height of some small patch of the surface, although it may not be maximum overall.

We further define f( x,y) to have a local minimum at a point ( p,q) if -f( x,y) has a local maximum at ( p,q) .

To find the local extrema of a function of two variables which is smooth everywhere, we first notice that the tangent plane to the graph of f(x,y) is horizontal at a local maximum or local minimum.

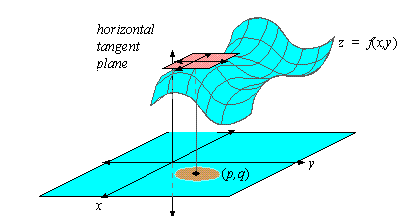
However, the linearization of f( x,y) at ( p,q) is of the form

Definition 6-1: The critical points of a function f(x,y) are those points ( p,q) for which

fx( p,q) = 0        and        fy(p,q) = 0

By the discussion above, the extrema of f( x,y) must occur at its critical points.       

EXAMPLE 1    Find the critical point(s) of

f( x,y) = x3-3xy+y3

Solution: The first partial derivatives are

fx( x,y) = 3x2-3y,        fy( x,y) = -3x+3y2

Setting f_x and f_y equal to zero leads to 2 simultaneous equations:

3x2-3y = 0,        -3x+3y2 = 0

Simplifying leads to y = x² and x = y², which implies that x = x⁴. Since x = x⁴ is the same as x⁴-x = 0, we obtain

x( x3-1)  =  0 x( x-1) ( x2+x+1)  =  0

which results in x = 0 and x = 1. Since y = x², we have x = 0 implies y = 0, while x = 1 implies y = 1. Thus, the critical points are (0,0) and ( 1,1) .

Graphic of Directional Derivative