The Second Derivative Test   

Clearly, f( x,y) has a local maximum at a critical point ( p,q) only if every vertical slice of z = f(x,y) has a maximum at ( p,q) .

Similarly, f( x,y) has a local minimum at a critical point ( p,q) only if every vertical slice of z = f( x,y) has a minimum at ( p,q) .

However, it is possible for f( x,y) to have a minimum in one slice and a maximum in another slice.

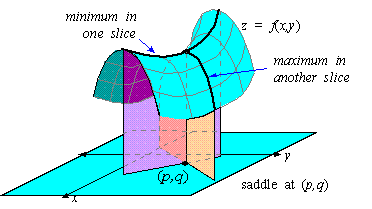
If this is the case, then we say that f( x,y) has a saddle at ( p,q) , because the resulting surface resembles a saddle for a horse.

To determine if we get a maximum, a minimum, or a saddle point at a critical point ( p,q) , consider the vertical slice z( t) = f( p+mt,q+nt) . Then x = p+mt and y = q+nt implies that x' ( t) = m and y' ( t) = n. As a result, the chain rule yields

dz dt =  ¶f ¶x  dx dt +  ¶f ¶y  dy dt = mfx+nfy

Moreover, m and n constant implies that

z" ( t) = m  dfx dt +n  dfy dt = m æ è  ¶fx ¶x  dx dt +  ¶fx ¶y  dy dt ö ø +n æ è  ¶fy ¶x  dx dt +  ¶fy ¶y  dx dt ö ø = m( mfxx+nfxy) +n( mfyx+nfyy)

Expanding and using the equality of the mixed partial derivatives then yields

z"( 0) = m2fxx( p,q)+2mnfxy( p,q) +n2fyy( p,q)

(1)

In elementary algebra, it is shown that an expression of the form am²+bmn+cn² has the same sign for all m and n only if b²-4ac < 0. Thus, z"( 0) in (1) has the same sign for all m and n ony if

4[ fxy( p,q) ] 2-4fxx( p,q)fyy( p,q) < 0

This reduces to f_xx( p,q) f_yy( p,q) -[f_xy( p,q) ] ² > 0, which motivates us to define the discriminant of f( x,y) to be

D( x,y) = fxxfyy-[ fxy] 2

Thus, f( x,y) has a maximum at ( p,q) if f_xx( p,q) < 0 and D( p,q) > 0, a minimum at ( p,q) if f_xx( p,q) > 0 and D( p,q) > 0, and a saddle at ( p,q) when z"(0) has different signs in different vertical slices, which is when D( p,q) < 0.           

Second Derivative Test: If ( p,q) is a critical point of a function f( x,y) whose second derivatives exist at ( p,q) , then

a) If D( p,q) > 0 and fxx( p,q) > 0 then f( x,y) has a local minimum at ( p,q) b) If D( p,q) > 0 and fxx( p,q) < 0 then f( x,y) has a local maximum at ( p,q) c) If D( p,q) < 0, then f( x,y) has a saddle at ( p,q) d) If D( p,q) = 0, then no information about f( x,y) is obtained

The second derivative test can be extended to functions of more than one variable by noticing that the discriminant is the determinant of the Hessian H_f( p,q) (see Maple worksheets for an exploration of this idea).       

EXAMPLE 2    Identify the extrema and saddle points of f(x,y) = x²-y².      

Solution: Since f_x = 2x and f_y = -2y, the only critical point is ( 0,0) . However, f_xx = 2, f_yy = -2, and f_xy = 0, so that the discriminant of f is

D = fxxfyy-( fxy) 2 = ( 2) ( -2)-02 = -4 < 0

Thus, f( x,y) = x²-y² has a saddle at ( 0,0) .

EXAMPLE 3    Find the extrema and saddle points of f(x,y) = x³-3xy+y³.   

Solution: In example 1, we showed that the critical points of f are ( 0,0) and ( 1,1) . Since f_x(x,y) = 3x²-3y and f_y( x,y) = -3x+3y², the second derivatives of f( x,y) are

fxx = 6x,        fxy = -3,        fyy = 6y

Thus, the discriminant is

D( x,y) = ( 6x) ( 6y) -( -3)2 = 36xy-9

At ( 0,0) , we have D( 0,0) = 0-9 = -9 < 0. Thus, f has a saddle at ( 0,0) . At ( 1,1) , we have

D( 1,1) = 36·1·1-9 = 27 > 0

However, f_xx( 1,1) = 6 > 0, so f has a local minimum at ( 1,1) .