Example 4
Find the point on the intersection of the plane
z=
3
x+
4
y+
6 and the paraboloid
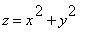 which is closest to the origin.
which is closest to the origin.
![[Maple Plot]](images/2-965.gif)
(commands used to generate figure above)
Example 4
Find the point on the intersection of the plane
z=
3
x+
4
y+
6 and the paraboloid
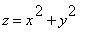 which is closest to the origin.
which is closest to the origin.
![[Maple Plot]](images/2-965.gif)
(commands used to generate figure above)
Solution:
The equation of the plane and the equation of the paraboloid are the constraints. Our objective is to minimize the square of the distance from a point ( x,y,z ) to the origin. Thus, our constrained optimization problem is of the form
Minimize
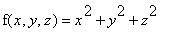
subject to 3
x+
4
y+
6
- z
= 0 and
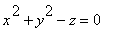
Thus, the Lagrangian is as follows:
| > | Lagrangian:=x^2+y^2+z^2+lambda[1]*(3*x+4*y+6-z)+lambda[2]*(x^2+y^2-z); |
| > |
Next we set the gradient equal to 0 and solve:
| > | grad(Lagrangian,[x,y,z,lambda[1],lambda[2]]); convert(%,'set'): sols:=[solve(%,{x,y,z,lambda[1],lambda[2]})]; |
| > |
There are two solutions in this case.
| > | solution1:=sols[2]; solution2:=sols[3]; |
| > |
Let's now evaluate f at each of these points:
| > | seq(print("At ",sols[j],": f(x,y,z) = ",subs(sols[j],x^2+y^2+z^2)),j=2..3); |
| > |
Clearly, the closer of these two points is
(
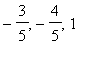 )
)
which is shown as a black point in the plot below:
| > | p1:=plot3d(3*x+4*y+6,x=-2..2,y=-x-2..-x+2,color=red,grid=[5,5]): p2:=plot3d(x^2+y^2,x=-2..2,y=-sqrt(4-x^2)..sqrt(4-x^2)): p3:=sphere([-3/5,-4/5,1],0.1,color=black,grid=[10,10]): display(p1,p2,p3,view=[-2..2,-2..2,0..7],axes=normal); |
| > |