Lagrange Multipliers and Level Surfaces

A function F ( x,y,z ) assigns a numerical value--i.e., a scalar--to each point in 3-dimensional space.  For that reason, F ( x,y,z ) is often called a scalar field, and it is typical to desire to find the extrema of a scalar field.  For example, let's suppose that

  T ( x,y,z ) =     

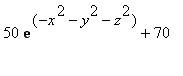
assigns temperatures in degrees Fahrenheit to each point in xyz -space. Thus, the temperature at the origin is T (0,0,0) = 120 degrees.  It would be natural to ask what the hottest and coldest points in space are.  

Moreover, we often desire to find extrema of scalar fields on a level surface U ( x,y,z ) = k .  In this case, the level surface is a constraint  and the optimization problems are Lagrange multiplier problems.  For example, the question "What point(s) on the surface U ( x,y,z ) = k  are closest to the origin?"  requires us to

minimize   F ( x,y,z ) =

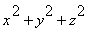
  subject to the constraint U ( x,y,z )  = k   

since   F ( x,y,z ) = 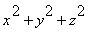 is the square of the distance from the point ( x,y,z ) to the origin.

Example

Let's find the point(s) on the hyperboloid 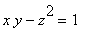    that are closest to the origin.  To begin with, we write the constraint as 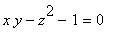 and then use it and F  to construct a Lagrangian function.

>	Lagrangian:=x^2+y^2+z^2-lambda*(x*y-z^2-1);

>

Next we must calculate the gradient of the Lagrangian.  The point(s) where the gradient of the Lagrangian vanishes (i.e., is equal to 0) are points where the least and greatest distances must occur, if they do occur.

>	grad(Lagrangian,[x,y,z,lambda]); convert(%,'set'): solve(%,{x,y,z,lambda});

>

Since 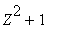 has no real roots, only two real-valued solutions occur--namely, (1,1,0) and (-1,-1,0).   At these points, we have

F (1,1,0) = F (-1,-1,0) = 2

Let's plot these points along with the surface:

>	p1:=implicitplot3d(x*y-z^2=1,x=-2..2,y=-2..2,z=-2..2): p2:=sphere([1,1,0],0.1,color=blue): p3:=sphere([-1,-1,0],0.1,color=blue): p4:=sphere([0,0,0],0.1,color=black): p5:=textplot3d([0,0.25,0,"(0,0,0)"],color=black): display(p1,p2,p3,p4,p5);

>

Although we have not proven so directly, it is safe to conclude that (1,1,0) and (-1,-1,0) are the points on the hyperboloid that are closest to the origin.

Let's conclude with an example from physics and engineering, where Lagrange multipliers play a key role in modeling real world phenomena.  In particular, Lagrange multipliers allow us to form theoretical models in empty space, and then constraints are used to restrict those models to a given surface or solid.  

Notice that in this next example, the constraint is an entire surface and we are now using an additional variable.

Example

A sphere of radius 1 centered at (3,4,0) is subjected to a gravitational potential field whose source is a point mass located at the origin.  Thus, the potential energy is

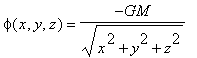
where G  is the universal gravitational constant and M is the mass of the point-mass located at the origin.  What points on the surface of the sphere have the least and the greatest gravitational potential with respect to the point mass?

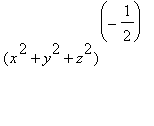Solution:   We must find the extrema of ( x,y,z ) = k  where k=-GM  is a constant.    Our constraint that the point ( x,y,z ) is on the sphere.  Thus, our Lagrangian is

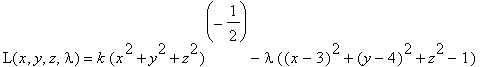
Let's compute its gradient and set it equal to 0.

>	Lagrangian:=k*(x^2+y^2+z^2)^(-1/2)-lambda*((x-3)^2+(y-4)^2+z^2-1); grad(Lagrangian,[x,y,z,lambda]); convert(%,'set'): solve(%,{x,y,z,lambda});

>

Thus, the extrema for the gravitational potential on the sphere due to a point-mass at the origin are located at the points

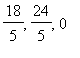( )  and    ( )
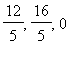