and latitude
, which is given by
Parametrizations of the Sphere
Although parametric equations can be used to define some extremely interesting surfaces, it is no less important that there are many, many different parametrizations of the same surface. There is perhaps no surface for which this idea is more important than the unit sphere.
For example, one of the most common parametrizations of the sphere is in terms of longitude
and latitude
, which is given by
r
(
) = < cos(
) cos(
), sin(
) cos(
), sin(
) >
It also produces perhaps the most familiar visualization of the sphere.
> plot3d([cos(theta)*cos(phi),sin(theta)*cos(phi),sin(phi)],theta=0..2*Pi,phi=-Pi/2..Pi/2,scaling=constrained);
>
There are, however, many other parametrizations of the sphere. For instance, the hyperbolic functions
tanh(
v
) =
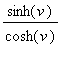and sech(
v
) =
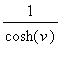
satisfy the identity
(
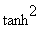v
) +
(
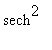v
) = 1. The
Mercator
projection is defined in terms of these by
r
() = < sech(
v
) cos(
), sech(
v
) sin(
), tanh(v)>
then
(
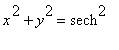v
) and consequently,
(
v
) +
(
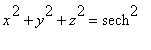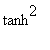v
) = 1.
Thus, the Mercator projection is a parametrization of the sphere.
> plot3d([sech(v)*cos(theta),sech(v)*sin(theta),tanh(v)],theta=0..2*Pi,v=-4..4,scaling=constrained);
>
Another important parametrization of the sphere is called stereographic projection. In particular, if we imagine that the uv -plane passes through the equator of the
unit sphere, then the line segment from a point ( u,v ) to the north pole at (0,0,1) passes through the sphere at exactly one point ( x,y,z ).
![[Maple Bitmap]](images/3-236.gif)
Right triangles and some straightforward geometry can then be used to show that ( x,y,z ) can be expressed in terms of ( u,v ) by the formulas
,
,
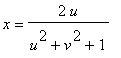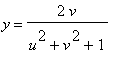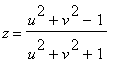
As a result, the stereographic parametrization of the plane is given by
r
(
u,v
) =
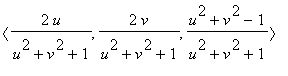
It is shown below except for a small spherical cap about the north pole.
> plot3d([2*u/(u^2+v^2+1),2*v/(u^2+v^2+1),(u^2+v^2-1)/(u^2+v^2+1)],u=-4..4,v=-sqrt(16-u^2)..sqrt(16-u^2),grid=[50,50],scaling=constrained);
>