Exercises

Use a graphing calculator or computer algebra system to sketch each surface and then find the level surface representations of each of the following parametric equations.

1. r = á vsin( u) ,vcos( u),v ñ 2. r = á vsin( u),v,vcos( u) ñ 3. r = á sin( u) cos( v),cos( u) ,sin( u) sin( v) ñ 4. r = á sin( v) sin( u) ,cos( v) sin( u) ,cos(u) ñ 5. r = á 2sin( u) cos( v),3cos( u) ,2sin( u) sin( v) ñ 6. r = á 2sin( u)cos( v) ,2cos( u) ,sin( u) sin( v) ñ 7. r = á sin( u) cosh( v),sinh( v) ,cos( u) cosh( v) ñ 8. r = á sin( u)cosh( v) ,sin( u) sinh( v) ,cos( u) ñ 9. r = á sec( u) sin( v),sec( u) cos( v) ,tan( u) ñ 10. r = á vsin( u),vcos( u) ,v2sin( 2u) ñ 11. r = á evsin( u) ,evcos(u) ,e-v ñ 12. r = á sin( v) cos( u) ,sin( v) sin(u) ,sin2( v) cos( 2u) ñ

Find r_u and r_v for each of the following surfaces. Compute their dot product to determine if the parametrization is orthogonal or not.

13. r = á vsin( u) ,vcos( u),uv ñ 14. r = á vsin( u),v2,vcos( u) ñ 15. r = á sin( u) cos( v),cos( u) ,sin( u) sin( v) ñ 16. r = á sin( v)sin( u) ,cos( v) sin( u) ,cos(u) ñ 17. r = á evsin( u) ,evcos(u) ,e-v ñ 18. r = á 2sin( u) cos( v) ,2cos( u) ,sin(u) sin( v) ñ

Find the equation of the tangent plane to r(u,v)  at the point r( p,q) for the given ( p,q) . 

19. r = á vsin( u) ,vcos( u),uv ñ 20. r = á vsin( u),v2,vcos( u) ñ ( p,q) = ( p/3,1) ( p,q) = ( p/4,1) 21. r = á vsin( u) ,vcos( u),v ñ 22. r = á sin( v)sin( u) ,cos( v) sin( u) ,cos(u) ñ ( p,q) = ( p/6,2) ( p,q) = ( p/3,p/4) 23. r = á evsin( u) ,evcos(u) ,e-v ñ 24. r = á sin( u) cosh( v) ,sin( u) sinh(v) ,cos( u) ñ ( p,q) = ( p,1) ( p,q) = ( p,ln2)

Find the surface of revolution obtained by revolving the following surfaces about the x-axis. Then find r_u and r_v and determine if the parametrization is orthogonal.

25. y = x,  x in [ 0,1] 26. y = x+1,  x in [0,1] 27. y = x-x2, x in [ 0,1] 28. y = x-x3, xin [ 0,1] 29. y = cosh( x) , x in [ -1,1] 30. y = sin( x) , x in [ 0,p]

31. The helicoid is the surface parametrized by

r( u,v) = á sinh( v) cos(u) ,sinh( v) sin( u) ,u ñ

Graph the helicoid for (u,v) in [0,2p]×[0,1].  How is the helicoid related to a helix?  Is the parametrization orthogonal?

32. A catenoid is the surface parametrized by

r( u,v) = á cosh( v) cos(u) ,cosh( v) sin( u) ,v ñ

Graph both the catenoid and the helicoid in exercise 31.  How are they similar?  How do they differ?

33. A Mobius strip is a surface parametrized by

r( u,v) = 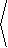cos( u) +vcos æ è  u 2 ö ø cos( u) ,sin( u) +vcos æ è  u 2 ö ø sin( u) ,vsin æ è  u 2 ö ø

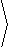for u in [ 0,2p] and v in [ -0.3,0.3] . Graph the Mobius strip with either a graphing calculator or a computer. What is the parametrization of its tangent plane when u = p and v = 0.1? (see problem 31)

34. Show that every parametric equation of the form

r( u,v) = á f( v) cos(u) ,f( v) sin( u) ,f( v) ñ

is a parametrization of a section the cone x²+y² = z². Is the parametrization orthogonal?

35. Use an identity for the hyperbolic trigonometric functions to prove that

sech2( A) +tanh2( A) = 1

Then show that the Mercator parametrization

r( q,m) = á R sech( m) cos( q) ,R sech( m) sin( q) ,Rtanh( m) ñ

is indeed a parametrization of the sphere of radius R centered at the origin.

36. Show that r( t,u,v) = á sin( t) cos( v) ,cos( t) cos(v) ,sin( u) sin( v) ,cos( u)sin( v) ñ is a parametrization of the sphere in 4 dimensions given by

x2+y2+z2+w2 = 1

37. Find another parametrization of the sphere of radius R centered at the origin by revolving the upper half circle

y = R2-x2 ,    x  in  [ -R,R]

about the x-axis. Is the parametrization orthogonal?

38. If a curve r( v) = á 0,f(u) ,g( u) ñ for u in [ a,b] is revolved about the y-axis, then the resulting surface of revolution is parametrized by

r( u,v) = á g( u) sin(v) ,f( u) ,g( u) cos( v) ñ

where ( u,v) is in[ a,b] ×[ 0,2p] .

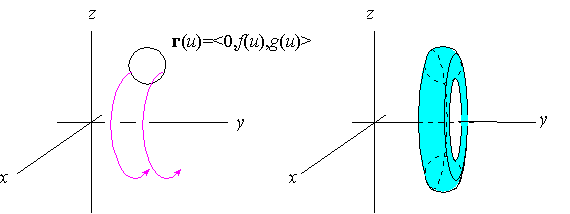
Find the parametrization of the torus which results from revolving the circle

39. Determine the longitude q₀ and latitude j₀ of your present location, and then use (2) to find r_q, r_j, and the equation of the tangent plane to the earth at your location.

40. Write to Learn: Find the formula for revolving y = f(x) , x in [ a,b] , about the z-axis. Present and explain your formula in a short essay.

41.  Write to Learn:  Stereographic projection assigns to each point (u,v,0) the point ( x,y,z) on the unit sphere that is on the line from the point (0,0,1) through the point (u,v,0) .

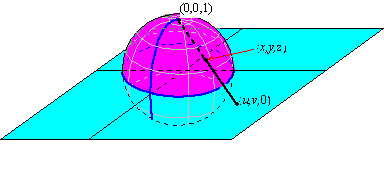
Use similar right triangles to show that stereographic projection leads to the following parameterization of the sphere.

r( u,v) =  2u u2+v2+1 ,  2v u2+v2+1 ,  u2+v2-1 u2+v2+1