Parametric Surfaces

Surfaces can also be defined parametrically. In particular, suppose each component of a vector-valued function is a function of two variables u and v:

r(u,v) = á f(u,v) ,g(u,v) ,h(u,v) ñ

(1)

Then the graph of r( u,v) over some region S in the uv-plane is a surface in R³, and r( u,v) is called a parameterization of that surface.

Equivalently, x = f(u,v) , y = g( u,v) , and z = h( u,v) for (u,v) in S defines a surface, and the variables u and v are often called the coordinates of the surface.

Given a parametric surface (1), we often desire to transform it into a level surface representation of the form U(x,y,z) = k. To do so, we often use the trigonometric identities, such as the Pythagorean identities

cos2( t) +sin2( t) = 1 1+tan2( t) = sec2( t) 1-2sin2(t) = cos( 2t) cosh2( t) -sinh2( t) = 1 1+cot2( t) = csc2( t) 2cos2(t) -1 = cos( 2t)

Other identities that may occur include 2sin( t) cos(t) = sin( 2t) and e^te^-t = 1.       

EXAMPLE 1    Find a level surface representation of the surface parameterized by

r( u,v) = á cos( u) cosh(v) ,sin( u) cosh( v) ,sinh( v) ñ

Solution: Since x = cos( u) cosh( v) , y = sin( u) cosh( v) , and z = sinh( v), the identity cos²( u) +sin²( u) = 1 leads to

x2+y2 = cos2( u) cosh2( v) +sin2( u) cosh2( v) = cosh2( v) [ cos2( u) +sin2( u) ] = cosh2( v)

As a result, the identity cosh²( v) -sinh²(v) = 1 leads to

x2+y2-z2 = cosh2( v) -sinh2( v) = 1

Thus, r( u,v) = á cos( u) cosh( v) ,sin( u) cosh( v) ,sinh(v) ñ is a parameterization of the level surface

x2+y2-z2 = 1

which we recognize as a hyperboloid in one sheet.

Graphic of Directional Derivative

       

A sphere of radius R centered at the origin is often parameterized in terms of longitude q and latitude j, which results in the parameterization

r( q,j) = á Rcos( j) cos( q) ,Rcos( j) sin(q) ,Rsin( j) ñ

(2)

where q in [ 0,2p] and j is in [-p/2,p/2] .

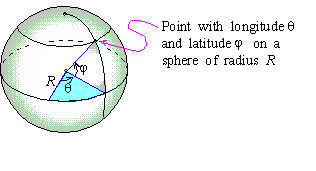
EXAMPLE 2    Show that (2) is a parameterization of the sphere of radius R centered at the origin.       

Solution: Since x = Rcos( j) cos( q) , y = Rcos( j) sin( q) and z = Rsin( j) , the identity cos²( q) +sin²( q) = 1 leads to

x2+y2 = R2cos2( j) cos2( q) +R2cos2( j) sin2( q) = R2cos2( j) [ cos2( q) +sin2( q) ] = R2cos2( j)

Moreover, z² = R²sin²( j) implies that

x2+y2+z2 = R2cos2( j) +R2sin2(j) = R2

which is the equation of the sphere of radius R centered at the origin.

However, cartographers and mathematicians have long used parameterizations of the sphere other than (2). For example, in 1599, the mapmaker Gerard Mercator constructed a projection of the earth's surface in which a straight line on a map corresponds to a fixed compass bearing on the earth's surface. To do so, he imagined that the sphere was inside of a cylinder with radius R.

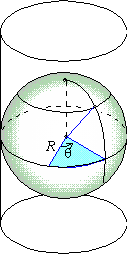
This led to the Mercator parameterization of the sphere: