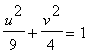Rotations and Conics

Rotation about the origin through an angle is a linear transformation of the form

T

We can use Maple to animate rotation through an angle of of a curve or a region. For example, let's look at rotation of the unit square about the origin.

> plot_array:=array(1..73):
plot_array[1]:=polygon([[0,0],[1,0],[1,1],[0,1]],color=cyan,scaling=constrained):
T:=transform((u,v)->[cos(5/180*Pi)*u-sin(5/180*Pi)*v,sin(5/180*Pi)*u+cos(5/180*Pi)*v]):
for i from 1 to 72 by 1 do
plot_array[i+1]:=T(plot_array[i]):
title_string:=cat("q=",i*5):
plot_array[i+1]:=display(plot_array[i+1],title=title_string,titlefont=[SYMBOL,12]):
end do:
plot_array[1]:=display(plot_array[1],title="q=0",titlefont=[SYMBOL,12]):
display(seq(plot_array[i],i=1..73),insequence=true);

>

As an application of this technique, let's suppose we are given a conic whose major and minor axes are at some unknown angle to the x and y axes. Rotation through some particular value of angle will lead to the conic's axes coinciding with the x and y axes, thus allowing us to identify the semi-major and semi-minor axes of the conic.

Let's look at an example. Let's rotate the conic

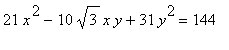
through various values of to discover its semi-major and semi-minor axes. In particular, rotation of the conic in the clockwise direction will cancel an original rotation in the counterclockwise rotation. Thus, we want to determine how much rotation in the clockwise direction is needed to place the curve in standard position.

> #Enter curve of the form g(x,y)=k
conic_curve:=21*x^2-10*sqrt(3)*x*y+31*y^2=144:

#Rotation of conic through 5 degree increments
plot_array:=array(1..72):
plot_array[1]:=implicitplot(conic_curve,x=-5..5,y=-5..5,scaling=constrained):
T:=transform((u,v)->[cos(5/180*Pi)*u+sin(5/180*Pi)*v,-sin(5/180*Pi)*u+cos(5/180*Pi)*v]):
for i from 1 to 71 by 1 do
plot_array[i+1]:=T(plot_array[i]):
title_string:=cat("q=",i*5):
plot_array[i+1]:=display(plot_array[i+1],title=title_string,titlefont=[SYMBOL,12]):
end do:
plot_array[1]:=display(plot_array[1],title="q=0",titlefont=[SYMBOL,12]):
display(seq(plot_array[i],i=1..72),insequence=true,scaling=constrained);
#Stop the animation when the conic is in standard position:

>

Rotation through an angle of 30 degrees reveals the length of the semi-major and semi-minor axes. It follows that if we substitute for x and y using the rotation tranformation with , then the simplified result will be the conic in a standard form.

> simplify(expand(subs(x=cos(30*Pi/180)*u-sin(30*Pi/180)*v,y=sin(30*Pi/180)*u+cos(30*Pi/180)*v,conic_curve)));

>

Thus, the unrotated conic section is of the form