Exercises:

Find the image in the xy-plane of the given curve in the uv-plane under the given transformation. If the transformation is linear, identify it as such and write it in matrix form.
1.
T( u,v) = á u,v2 ñ , v = 2u
2.
T( u,v) = á uv,u+v ñ , v = 3
3.
T( u,v) = á u-2v,2u+v ñ , v = 0
4.
T( u,v) = á u+3,v+2 ñ , u2+v2 = 1
5.
T( u,v) = á 4u,3v ñ , u2+v2 = 1
6.
T( u,v) = á u2+v,u2-v ñ , v = u
7.
T( u,v) = á u2-v2,  uv ñ , v = 2
8.
T( u,v) = á u2-v2,2uv ñ , u = -1
9.
T( r,q) = á rcos( q),rsin( q) ñ ,  r = 1
10.
T(r,q) = á rcos( q) ,rsin(q) ñ ,  q = p/4

Find the coordinate curves of the given transformation. Then find the image of the unit square in the uv-plane under the given transformation. If the transformation is linear, identify it as such and write it in matrix form.
11.
T( u,v) = á u+1,v+5 ñ
12.
T( u,v) = á 2u+1,3v-2 ñ
13.
T( u,v) = á v,u ñ
14.
T( u,v) = á u+v+1,v+2 ñ
15.
T( u,v) = á u2-v2, u + v ñ
16.
T( u,v) = á u2+v,u2-v ñ
17.
T( u,v) = á 2u+3v,-3u+2v ñ
18.
T( u,v) = á ucos( pv) ,usin(pv) ñ
19.
Rotation about the origin
20.
Rotation about the origin
through an angle q =  
p
4
through an angle q =  
2p
3
21.
T( u,v) = á uev,ue-v ñ
22.
T( u,v) = á u + v, u + v ñ
23.
T( r,q) = á rcos( q),r2sin2( q) ñ
24.
T(r,t) = á rcosh( t) ,rsinh( t) ñ

Find a conic in standard form that is the pullback under rotation of the given curve. (You found the principal axes for these conics in section 2-9).
25.
5x2+6xy+5y2 = 8
26.
5x2-6xy+5y2 = 8
27.
xy = 1
28.
xy = 4
29.
7x2+6xÖ3y+13y2 = 16
30.
13x2-6xÖ3y+7y2 = 16

       

31. For the conic 52x2-72xy+73y2 = 100, show that tan(q) = 3/4. Then explain why
cos( -q) =  4
5
     and    sin( -q) =  -3
5
and find the pullback under rotation through angle q of the given conic.

32. Find tan( q) for 73x2+72xy+52y2 = 100 and use it to determine cos(q) and sin(q) (see #31). Then find the pullback under rotation through angle q of the given conic.

33. Show that if
é
ê
ë
x
y
 ù
ú
û 		= é
ê
ë
cos( q)
-sin( q)
sin( q)
cos( q)
 ù
ú
û 		é
ê
ë
u
v
 ù
ú
û
then we must also have
é
ê
ë
u
v
 ù
ú
û 		= é
ê
ë
cos( q)
sin( q)
-sin( q)
cos( q)
 ù
ú
û 		é
ê
ë
x
y
 ù
ú
û
What is the significance of this result?

34. Use matrix multiplication to show that a rotation through an angle q followed by a rotation through an angle f is equivalent to a single rotation through the angle q+f.

35. The parabolic coordinate system on the xy-plane is the image of the coordinate transformation
T( u,v) = á u2-v2,2uv ñ
Find the image of the horizontal lines u = 0,1,2 and the vertical lines v = 0,1,2 in the parabolic coordinate system.

36. The tangent coordinate system on the xy-plane is the image of the coordinate transformation
T( u,v) =
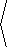
 u
u2+v2
 ,   v
u2+v2
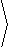Find the image of the horizontal lines u = 0,1,2 and the vertical lines v = 0,1,2 in the tangent coordinate system.

37. The elliptic coordinate system on the xy-plane is the image of the coordinate transformation
T( u,v) = á cosh( u) cos( v),  sinh( u) sin( v) ñ
Find the image of the horizontal lines u = 0,1,2 and the vertical lines v = 0,1,2 in the elliptic coordinate system.

38. The bipolar coordinate system on the xy-plane is the image of the coordinate transformation
T( u,v) =
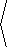
 sinh( v)
cosh(v) -cos( u)
,  sin( u)
cosh(v) -cos( u)
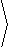Find the image of the horizontal lines u = 0,1,2 and the vertical lines v = 0,1,2 in the bipolar coordinate system.

39. Write to Learn: A coordinate transformation T( u,v) = á f( u,v), g( u,v) ñ is said to be area preserving if the area of the image of any region S in the uv-plane is the same as the area of R. Write a short essay explaining why a rotation through an angle q is area preserving.

40. Write to Learn: What type of coordinate system is implied by the coordinate transformation T( u,v) = á u, F(u) + v ñ?  What are the coordinate curves?  What is significant about tangent lines to these curves?  Write a short essay which addresses these questions.  

41.  Simplify (4) into (5) using the double angle formula for the tangent function.