Rotation of Conics into Standard Form

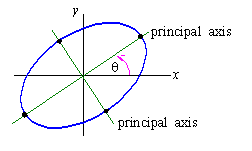
The prinicipal axes of a conic of the form
Ax2+Bxy+Cy2 = k
(2)
in the xy-plane are the axes which contain the points closest to and fathest from the origin.

Our goal is to rotate the conic into standard form, or more accurately, to find the conic in standard form that is rotated to produce the given conic.  

In section 2-9, we saw that the principal axes contain the points closest to and farthest from the origin.  Thus, to find the principal axes for (2), we find the extrema of f( x,y) = x2+y2 with (2) as the constraint.   Lagrange multipliers subsequently yields

Ñg = lÑf    Þ     á2Ax+By,Bx+2Cy ñ = l á 2x,2y ñ
Thus, 2Ax+By = l2x and Bx+2Cy = l2y, so that
2Axy+By2 = l2xy = Bx2+2Cxy
Solving for y in 2Axy+By2 = Bx2+2Cxy yields
y =
C-A±
( C-A) 2+B2
B
   x
(3)

Let us now let q be the angle formed by one of the principal axes with the x-axis (see the figure above). Then tan( q) is the slope of that axis, so that comparison to (3) yields
tan(q) =
C-A±
( C-A) 2+B2
B
    
(4)
Incredibly, if we now substitute (4) into the double angle formula for the tangent function
tan( 2q) =  2tan( q)
1-tan2( q)
then (4) yields the much simpler form
tan( 2q) =  B
A-C
(5)

Thus, our conic in the xy-plane can be considered the image of a conic in standard position in the uv-plane.

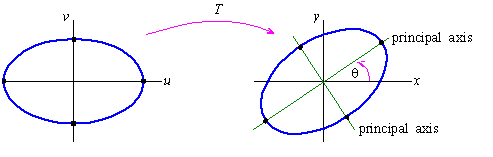
We say that the conic in the uv-plane is the pullback under rotation of the curve in the xy-plane.  

To compute the pullback, we use the rotation transformation

é
ê
ë
x
y
 ù
ú
û 		= é
ê
ë
cos( q)
-sin( q)
sin( q)
cos( q)
ù
ú
û 		é
ê
ë
u
v
 ù
ú
û
In particular, if we replace x and y in the original conic by
x
=
cos( q) u-sin( q) v
(6)
y
=
sin( q) u+cos( q) v
then simplifying the result will produce the pullback, which will be a conic in the uv-plane which is in standard form.     

EXAMPLE 7    Find the conic in standard form in the uv-plane which is the pullback under rotation of
7x2-6Ö3xy+13y2 = 16
Solution: Since A = 7, B = -6Ö3, and C = 13, formula (5) results in
tan( 2q) =  -6Ö3
7-13
 = Ö3
Thus, 2q = p/3, which implies that q = p/6 . As a result, the equations (6) lead to
x
=
cos æ
è 		 p
6
 ö
ø 		u-sin æ
è 		 p
6
 ö
ø 		v        Þ     x =  Ö3
2
 u-  1
2
 v
y
=
sin æ
è 		 p
6
 ö
ø 		u+cos æ
è 		 p
6
 ö
ø 		v        Þ     y =  1
2
 u+  Ö3
2
 v

Substitution into the original equation then leads to
7 æ
è 		 Ö3
2
 u-  1
2
 v ö
ø 		2

 
 -6Ö3 æ
è 		 Ö3
2
 u-  1
2
 v ö
ø 		æ
è 		 1
2
 u+  Ö3
2
 v ö
ø 		+13 æ
è 		 1
2
 u+  Ö3
2
 v ö
ø 		2

 
 = 16
Expanding and simplifying then leads to 4u2+16v2 = 16, so that in the uv-plane we have
 u2
4
 +  v2
1
 = 1
which is in standard form for an ellipse.