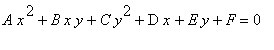
Conics in Polar Coordinates

A conic section is a curve of the form

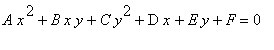
If B=0 , then the conic section is said to be in standard form .

Conic sections fall into 2 broad categories. Points and lines are called degenerate conics because they occur only for highly specialized choices of the coefficients. For example, lines occur when A=B=C=0 . Conic sections which are non-degenerate are classified as either ellipses, parabolas, or hyperbolas, with circles being special types of ellipses. For example, conic sections include circles centered at the origin ( A=C, B=D=E=0, , ) and parabolas with vertices at the origin ( , , B=C=D=F= 0 ).

We can learn a great deal about conic sections by converting them to graphs of functions in polar coordinates. To do so, we substitute and into the equation and solve for r. Let's look at an example:

Example: Convert to polar coordinates, graph, and describe the result.

Solution: To begin with, let's substitute and :

> x^2+y^2-2*y=5;
subs(x=r*cos(theta),y=r*sin(theta),%);
eq1:=simplify(%);

>

Now let's solve for r :

> solve(eq1,r);

>

Since we can always assume that r > 0, we choose the positive solution. The graph of the conic is shown below:

> polarplot(sin(theta)+sqrt(sin(theta)^2+5),theta=0..2*Pi,color=blue,scaling=constrained);

>

There are many other ways to define conic sections, as well. For example, given >0 and a vertical line l with equation x=-d where d>0 , a conic section can be defined to be all the points P for which | OP | = | lP|, where | lP | is the horizontal distance from the line to P and | OP | is the distance from P to the origin O.

As shown above right, the distance | OP | in polar coordinates is the same as the polar distance r . Moreover, the distance | lP | is given by

| lP | = d + r

Thus, the relationship | OP | = | lP| implies that

r = ( d + r )

Solving for r then leads to the equation of a conic in polar coordinates :

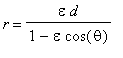
The line l is called the directrix of the conic and the number > 0 is called the eccentricity of the ellipse. Moreover, the origin is a focus of the ellipse.

If < 1, then the conic is an ellipse. If , then the conic is a parabola. If > 1, then the conic is a hyperbola. Let's explore this more closely using the following Maple Command group.

> #Enter a directrix value and an eccentricity
directrix:=1.5:
eccentricity:=0.7: #Must be positive!

# The commands below create the animation
parameter:=directrix*eccentricity:
pcenter:=parameter*eccentricity/(1-eccentricity^2):
amaj:=abs(pcenter/eccentricity):
extenty:=(abs(directrix)+amaj):
extentl:=pcenter-extenty:
extentr:=pcenter+extenty:
r:=parameter/(1-eccentricity*cos(theta)):
p1:=polarplot(r,theta=0..2*Pi,color=blue):
p2:=textplot([0.1,-0.1,"F"],align={BELOW,RIGHT}):
p3:=pointplot([0,0],symbol=circle,color=black):
dirplot:=plot([-directrix,t,t=-extent..extent],color=black):
dirtext:=textplot([-0.99*directrix,-directrix,"Directrix"],align={ABOVE,RIGHT},color=black):
for i from 1 to 20 by 1 do
if( abs(evalf(1-eccentricity*cos(i*Pi/10),5))>0) then
r_i:=subs(theta=i*Pi/10,r):
else
r_i:=extent:
end if:
x_i:=r_i*cos(i*Pi/10):
y_i:=r_i*sin(i*Pi/10):
if ( evalf(abs(x_i),5)>directrix+1 or evalf(abs(y_i),5)>directrix+1) then
x_i = x_i/abs(x_i)*extent:
y_i = y_i/abs(y_i)*extent:
end if:
pp2:=pointplot([x_i,y_i],color=black,symbol=circle):
pp3:=line([0,0],[r_i*cos(i*Pi/10),r_i*sin(i*Pi/10)],color=black):
pp4:=line([-parameter/eccentricity,r_i*sin(i*Pi/10)],
[r_i*cos(i*Pi/10),r_i*sin(i*Pi/10)],color=black):
if(evalf(sin(i*Pi/10),5)<0) then
pp5:=textplot([1.1*r_i*cos(i*Pi/10),1.1*r_i*sin(i*Pi/10),"P"],align=BELOW):
else
pp5:=textplot([1.1*r_i*cos(i*Pi/10),1.1*r_i*sin(i*Pi/10),"P"],align=ABOVE):
end if:
pp6:=textplot([-1.1*parameter/eccentricity,r_i*sin(i*Pi/10),"D"]):
dirfo[i]:=display(pp2,pp3,pp4,pp5):
end do:
ani:=display(seq(dirfo[i],i=1..20),insequence=true):
x_axis:=line([extentl,0],[extentr,0],color=black):
y_axis:=line([0,-extenty],[0,extenty],color=black):
display(p1,p2,dirplot,p3,dirtext,ani,x_axis,y_axis,scaling=constrained,axes=none,
view=[extentl..extentr,-extenty..extenty]);

>