Curves in Polar Coordinates

It is customary in polar coordinates to write the distance r as a function of q. In particular, r = f( q) assigns a distance from the origin to each angle q, thus forming a curve.

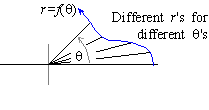
We can produce a rough sketch of a curve in polar coordinates by determining r at key angles, such as q = 0, p/6, p/4, p/3, p/2, 2p/3, etc., and  then plotting those points on a polar coordinate grid such as the one shown below:

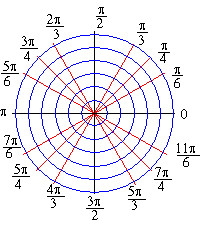
EXAMPLE 4    Sketch the graph of the function

r =  1 p q+1

Solution: First, let us choose some typical values of q and compute r for those angles.

q 0  p 4  p 2  3p 4 p  3p 2 2p 3p 4p r 1 1.25 1.5 1.75 2 2.5 3 4 5

Now let's plot those points on the grid and connect them to obtain a sketch of the graph of the function:

       

The fact that x = rcos( q) and y = rsin(q) implies that the graph of r = f( q) is parametrized by

r( q) = á f( q) cos( q) ,f( q) sin( q) ñ

This allows us to work with curves as parametric equations. In addition, it shows us that if f( q) is periodic with a period of 2p, then r( q) is a closed curve.  

EXAMPLE 5    Parametrize the graph of r = sin( 3q) for q in [ 0,2p] , and then sketch the resulting curve.       

Solution: A parametrization of the polar curve r = sin(3q) is given by

r( q) = á sin( 3q)cos( q) ,sin( 3q) sin( q) ñ

When q = 0 or q = 2p/3, then r = sin( 0) = sin( 3·2p/3) = 0. As a result,

r( 0) = r æ è  2p 3 ö ø = 0

which implies that r( q) is a closed curve on [ 0,2p/3] . Thus, the graph of r = sin( 3q) forms a single loop for q in [ 0,2p/3] . It then follows that it forms another loop when q is in [ 2p/3,4p/3] and yet another loop for q in [ 4p/3,2p] .

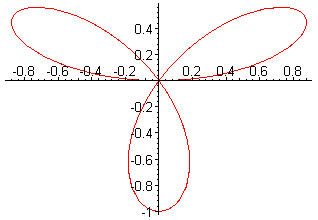
Since sin( 3q) has period 2p, the image of r = sin( 3q) is a closed curve.