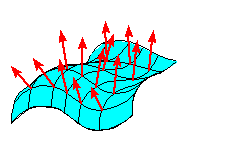
Orientability and the Surface Normal

The unit surface normal is defined for a level surface by normalizing the gradient.  That is, if U(x,y,z) = k is a level surface, then the unit surface normal is 

n =  ÑU || ÑU ||

If the level surface U(x,y,z) = k has a parameterization r(u,v), then either n or -n for the level surface is the same as the unit surface normal n defined in the previous section. 

If n varies continuously across a surface U(x,y,z) = k, then we say that U(x,y,z) = k is orientable.  Intuitively, orientability means that if the initial points of the unit surface normals n are placed on the surface, then their terminal points are all on the same side of the surface. If a surface is closed (such as a sphere), then we assume its orientation to be with all normal vectors pointing toward the outside of the surface.       

EXAMPLE 6    Explain why the surface z = x²cos(y) is orientable.   

Solution: Since z = x²cos( y) is the same as x²cos( y) -z = 0, we let U( x,y,z) = z-x²cos( y) , so that

ÑU = á -2xcos( y), x2sin( y), 1 ñ

Since the z-component of ÑU is 1, it is not possible for ÑU to ever be 0. In fact, because the z-component of ÑU is positive, all the normal vectors are above the surface z = x²cos(y) .

LiveGraphics3d Applet n drawn to 1/4 scale

Similarly, a parametric surface is orientable if n(u,v) varies continuously across the surface and if n( u,v) defines only one surface normal at each point on the surface. In particular, in a surface of revolution, orientable means the unit normal is 2p-periodic in q.

EXAMPLE 7    Find the unit surface normal of the surface

r( r,q) = á rcos( q), rsin( q) ,cosh( r) ñ

for q in [ 0,2p] and r in [ 0, 1] .  Explain why the surface is orientable.      

Solution: Since r_r = á cos( q) ,sin( q) ,sinh( r) ñ and r_q = á -rsin( q) ,rcos( q) ,0 ñ , their cross product is

rr×rq = á cos( q) ,sin( q) ,sinh( r) ñ×r á -sin( q) ,cos( q),0 ñ = r á - sinh( r) cos( q), -sinh( r) sin( q) ,1 ñ

The square of the magnitude of the cross product is

||rr×rq||2 = r2( sinh2( r) cos2( q)+sinh2( r) sin2( q) +1) = r2( sinh2( r) +1) = r2cosh2( r)

Thus, ||r_r×r_q|| = rcosh( r) , so that the unit normal is

n  =  rr×rq ||rr×rq||  =  r á -sinh(r) cos( q), -sinh(r) sin( q) ,1 ñ rcosh( r)  =  -sinh(r) cosh( r)  cos( q) , -sinh(r) cosh( r)  sin( q) , 1 cosh( r)  =  á - tanh( r) cos( q), -tanh( r) sin(q), sech( r) ñ

Since n( r,q) = á - tanh( r)cos(q), -tanh(r) sin(q), sech( r) ñ is continuous for all r and q, and since n( r,q) is 2p-periodic, the surface is orientable.

LiveGraphics3d Applet

Not all surfaces can be oriented. For example, a Möbius strip, which can be formed by twisting a strip of paper one half turn and pasting the two ends together, cannot be oriented.

Maple Graphics Export