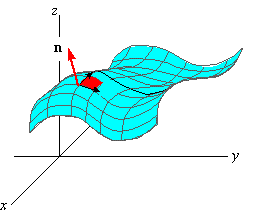
The Surface Normal

One of the most important concepts in studying surfaces is the concept of the unit normal to the surface. In particular, it will become prominent in chapter 5 as we generalize the fundamental theorem of calculus to more than one variable.

Suppose that r( u,v) is a regular parametrization of a surface. Since the crossproduct r_u×r_v is orthogonal to both r_u and r_v, the vector r_u×r_v is normal to the surface at r( u,v) . It follows that the unit vector

n =  ru×rv | | ru×rv| |

is also normal to the surface. The vector n is thus called the unit normal to the surface. It is important to note that n = n( u,v) is a function of u and v.      

EXAMPLE 1    Find the unit normal to the cylinder

r( u,v) = á cos( u) ,sin(u) ,v ñ

Solution: Since r_u = á -sin( u),cos( u) ,0 ñ = -sin( u) i+cos( u) j and since r_v = á0,0,1 ñ = k, their cross product is

ru×rv   =   ( -sin( u) i+cos( u) j) ×k   =   -sin( u) i×k+cos( u) j×k   =   sin( u) j+cos( u) i

That is, r_u×r_v = á cos(u), sin( u), 0 ñ . Moreover, | | r_u×r_v| | ² = cos²(u) + sin²( u) = 1, so that

n =  ru×rv || ru×rv || = á cos(u) ,sin( u) ,0 ñ

as is shown in the image below: Thus, at the point rotated u radians from the x-axis and v units vertically from the xy-plane, the normal to the cylinder is n = á cos(u), sin( u), 0 ñ.

Maple Graphics Export

If the surface is given in spherical or cylindrical coordinates, then we first use the relationships for x, y, and z, respectively, to obtain a parameterization of the surface. We will consider only cylindrical coordinates here. Spherical coordinates are included in the worksheet.       

EXAMPLE 2    Find the surface normal for the surface in cylindrical coordinates given by z = r+1.       

Solution: The function z = r+1 combined with x = rcos( q) and y = rsin( q) leads to the parameterization

r( r,q) = á rcos( q),rsin( q) ,r+1 ñ

Since r_r = á cos( q) ,sin(q) ,1 ñ and r_q = á-rsin( q) ,rcos( q) ,0 ñ , the cross product is

rr × rq = á -rcosq, -rsinq, r ñ

Moreover, || r_r×r_q|| = rÖ2, so that the surface normal is

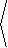
n =  rr×rq || rr×rq|| =  -cosq Ö2 ,  -sinq Ö2 ,  1 Ö2

       

 A surface S is said to be oriented if the surface normals at each point on the surface all point toward one side of the surface. Equivalently, a surface is oriented if n is uniquely defined at each point and varies continuously on the surface. (Not all surfaces can be oriented. For example, a Moebius strip, which can be formed by twisting a strip of paper one half turn and pasting the two ends together, cannot be oriented).

Maple Graphics Export