The Surface Normal for a Level Surface

In the first section, we saw that ÑU is normal to the level surface U( x,y,z) = k. Thus, the unit normal for a level surface is of the form
n =  ÑU
|| ÑU ||
at every regular point on the surface.      

EXAMPLE 3    What is the unit normal to the level surface
z = x2+y2
Solution: Since U( x,y,z) = x2+y2-z, the gradient is
ÑU = á 2x, 2y, -1 ñ
Thus, || ÑU || 2 =  4x2 + 4y2 + 1, so that
n =  ÑU
|| ÑU ||
=

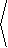
 2x
4x2+4y2+1
,  2y
4x2+4y2+1
,  1
4x2+4y2+1


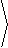
The unit normal is shown below at several different points (x,y,z) on the surface.

Maple Graphics Export


In cylindrical coordinates, a level surface is of the form U( r,q,z) = k. To find the surface normal to a surface in cylindrical coordinates, we must first determine a formula for the gradient in cylindrical coordinates. To begin with, we notice that
 U
r
=
 U
x
  x
r
 +  U
y
  y
r
 +  U
z
  z
r
 = cos(q) Ux+sin( q) Uy+0
 U
q
=
 U
x
  x
q
 +  U
y
  y
q
 +  U
z
  z
q
 = -rsin( q) Ux+rcos( q)Uy+0
If we now multiply Ur by cos( q) and multiply Uq by -sin( q) /r, then we obtain
cos( q)  U
r
=
cos2(q) Ux+sin( q) cos( q)Uy
-  sin( q)
r
  U
q
=
sin2( q) Ux-sin( q) cos( q) Uy
Combining the two equations leads to
cos( q)  U
r
 -  sin(q)
r
  U
q
 = ( cos2( q) +sin2( q) ) Ux = Ux
Similarly, it can be shown that Uy = sin( q)Ur+Uqcos( q) /r (see the exercises).

Consequently, the gradient in cylindrical coordinates is given by
ÑU = á Ux,Uy,Uz ñ =  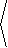 cos( q)  U
r
 -  sin( q)
r
  U
q
 ,sin( q)  U
r
 +  cos( q)
r
  U
q
 ,Uz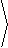
Let's now notice that we can write the gradient as
ÑU =  U
r
 á cos( q) ,sin( q) ,0 ñ +  1
r
  U
q
 á -sin( q) ,cos( q) ,0 ñ +  U
z
 á 0,0,1 ñ
If we thus let er = á cos( q) ,sin( q) ,0 ñ and let eq = á -sin( q) ,cos( q),0 ñ , then er, eq, and k are 3 mutually orthogonal unit vectors that form a basis for cylindrical coordinates, much as the i, j, and k vectors form the basis for Cartesian coordinates.  However, notice that the basis vectors er, eq, and k change direction from point to point, unlike the i, j, and k vectors (drag the red point in each of the following applets).
LiveGraphics3d Applet              LiveGraphics3d Applet
Moreover, the gradient in cylindrical coordinates can be written
ÑU = Ur er+  1
r
 Uq eq+Uz k
thus allowing us to calculate the surface normal in cylindrical coordinates.      

EXAMPLE 4    The unit sphere in cylindrical coordinates is given by
r2+z2 = 1
Find the surface normal of the unit sphere in cylindrical coordinates.       

Solution: Let us let U( r,q,z) = r2+z2. Then Ur = 2r, Uq = 0, and Uz = 2z. Thus,
ÑU
=
Ur er+  1
r
 Uq eq+Uz k
=
2rer+0 eq+2z k
=
2r á cos( q) ,sin( q),0 ñ +0+2z á 0,0,1 ñ
=
á 2rcos( q) ,2rsin( q),2z ñ
The square of the magnitude of the gradient is
|| ÑU || 2
=
4r2cos2( q)+4r2sin2( q) +4z2
=
4r2+4z2
=
4( r2+z2)
=
4
since r2+z2 = 1. Thus, || ÑU|| = 2 and the surface normal of the sphere in cylindrical coordinates is
n =   ÑU
|| ÑU||
 =    á2rcos( q) ,2rsin( q) ,2z ñ
2
 = á rcos( q) ,rsin( q) ,z ñ

   

It is important to note that we can also obtain ÑU in cylindrical coordinates by calculating ÑU in Cartesian coordinates and then converting the resulting gradient vector into cylindrical coordinates.  To illustrate, consider that the unit sphere in example 4 is given by x2+y2+z2 = 1,  which has a gradient of   
ÑU = á 2x, 2y, 2z ñ
Thus, in Cartesian coordinates, n = á x, y, z ñ since the point (x,y,z) is on the unit sphere, and conversion to cylindrical coordinates results in
n =  á rcos( q),  rsin( q),  z ñ

Check Your Reading: What is n in example 4 if transformed to Cartesian coordinates?