DIFF GEOM: Geodesics

The material in this chapter brings us very close to an extremely important field of mathematics known as Differential Geometry.  The "DIFF GEOM" material at the end of this chapter and in a few places in chapter 5 comprises an introduction to this extremely important field.  The "DIFF GEOM" material may be omitted completely without compromising the course, but we felt that such proximity to this important body of mathematics justified including this material for those inclined to pursue it.

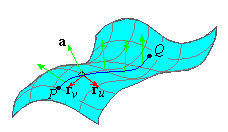
Let's begin with the concept of a geodesic.  Suppose that r( u,v) is the parameterization of a surface and that r( t) = r( u(t) ,v( t) ) is a curve on that surface.  If the acceleration r'' (t) is normal  to the surface at each point on the curve, then r( t) is said to be a geodesic on r( u,v). Equivalently, r( t) = r( u(t) ,v( t) ) is a geodesic only if r'' · r_u = 0 and r'' · r_v = 0. That is, a geodesic does not curve in any tangent plane to the surface, which means that geodesics are the ''straightest'' curves on a surface. The concept of a geodesic is illustrated by the animation below: Clicking on the animation will switch to a different view.

EXAMPLE 5    Let r( u,v) = á cos( u) ,sin( u) ,v ñ be a parameterization of the right circular cylinder, and let r( t) = r( t,2t+1) be a curve on that surface. Show that r( t) is a geodesic on the cylinder.      

Solution: The expression r( t,2t+1) implies that u = t and v = 2t+1. Thus, r( t) = ácos( t) ,sin( t) ,2t+1 ñ , so that

r' ( t) = á -sin( t),cos( t) ,2 ñ         and        r''( t) = á -cos( t),-sin( t) ,0 ñ

Since r_u = á -sin( u) ,cos(u) ,0 ñ and r_v = á0,0,1 ñ and since u = t, we have

r'' · ru = cos( t)sin( u) -cos( u) sin( t) = cos( t) sin( t) -cos( t) sin( t) = 0

Likewise, r'' ·  r_v = 0·cos( t) -0·sin( t) +2·0 = 0. Thus, r( t) = r( t, 2t+1) is a geodesic on the cylinder.

LiveGraphics3d Applet

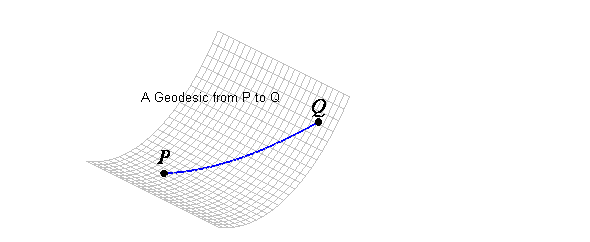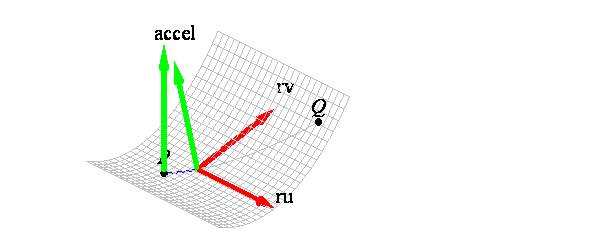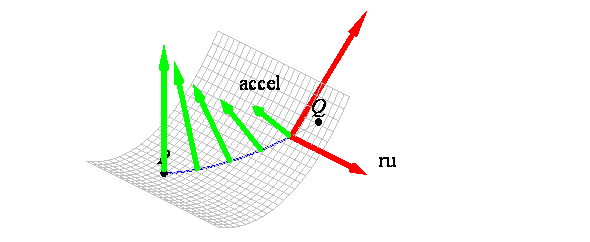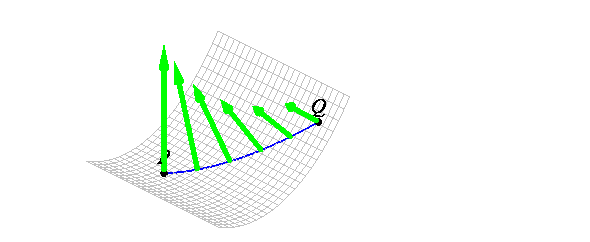
Since geodesics are the ''straightest'' curves on a surface, the shortest distance between two points must be along a geodesic, as is shown below assuming that the blue curve is the shortest curve on the surface from P to Q. This is especially important in applications involving surfaces such as the surface of the earth or a surface in curved ''space-time.''

For example, if r( u,v) is a parameterization of a sphere of radius R centered at the origin, then its unit normal n is parallel to r. Thus, a curve r(t) = r( u( t) ,v( t) ) is a geodesic on the sphere only if its acceleration is parallel to r(t) itself. However, r parallel to its acceleration is equivalent to

r'' (t) = l r( t)

for all t (and for some number l).  

Let's use this to simplify the derivative of  r( t) × r' ( t):  

d dt ( r( t) × r' ( t) ) = r' ( t) × r' ( t) + r(t) × r'' ( t) = 0+ r( t) ×l r(t) = 0

Consequently, r' ( t) × r' ( t) is constant and as a result, r(t) must lie in a plane through the origin. Thus, a geodesic on a sphere is a great circle, which is a circle formed by the intersection of the sphere with a plane through the sphere's center.

Drag the points to change the circle. (Thanks to Martin Kraus for this excellent applet).

EXAMPLE 6    Show that r( t) = r( p, t) is a geodesic on the sphere of radius R centered at the origin, where

r( q,j) = á Rcos( j) cos( q) ,Rcos( j) sin(q) ,Rsin( j) ñ

is the latitude-longitude parametrization of that sphere.       

Solution: The expression r( p, t) implies that q = p and j = t. Thus,

r( t) = á Rcos( t) cos( p) ,Rcos( t) sin( p) ,Rsin( t) ñ = á -Rcos( t) ,0,Rsin( t) ñ

It follows that its velocity and acceleration are

v( t) = á Rsin( t) ,0,Rcos( t) ñ         and        a(t) = á Rcos( t) ,0,-Rsin( t) ñ

Substituting q = p and j = t into the partial derivatives

rq = á -Rcos( j) sin( q) ,Rcos( j) cos( q) ,0 ñ rj = á -Rsin( j) cos( q) ,-Rsin( j) sin( q) ,Rcos( j) ñ

results in r_q( p,t) = á 0,-Rcos( t) ,0 ñ and r_j( p,t) = á Rsin( t) ,0,Rcos( t) ñ . Thus,

a · rq = Rcos( t) ·0-0·Rcos( t) -0·Rsin( t) = 0

Likewise, a · r_j = R²cos( t)sin( t) +0-R²sin( t) cos( t) = 0, which implies that r ( t) is geodesic on the sphere.

   

In addition, if r'' is normal to the surface, then the tangential acceleration of r( t) is zero and consequently, a geodesic r( t) has constant speed. For example, the speed of the geodesic in example 3 is Ö5 and the speed of the great circle in example 4 is 1. Since the speed of a geodesic is constant, the arclength is proportional to the parameter, and as a result, it is rather simple to obtain an arclength parameterization of a geodesic.