Part 1: Definition of the Integral

Iterated integrals are used primarily as a tool for computing double integrals, where a double integral is an integral of f( x,y) over a region R. In this section, we define double integrals and begin examining how they are used in applications.

To begin with, a set of numbers { x₀,x_j,r_j} , j = 1,¼,m, is said to be a tagged partition of [a,b] if

a = x0 < x1 < x2 < ¼ < xm = b

and if x_j-1 £ r_j £ x_j for all j = 1,...,m. Moreover, if we let Dx_j = x_j-x_j-1, then the partition is said to be h-fine if Dx_j £ h for all j = 1,¼,n.

If { x₀,x_j,r_j} , j = 1,¼,m, is an h-fine tagged partition of [ a,b] , and if {y₀,y_k,t_k} , k = 1,¼,n is a l-fine tagged partition of [ c,d] , then the rectangles [ x_j-1,x_j]×[ y_k-1,y_k] partition the rectangle [a,b] ×[ c,d] and the points (r_j,t_k) are inside the rectangles [ x_j-1,x_j]×[ y_k-1,y_k] .

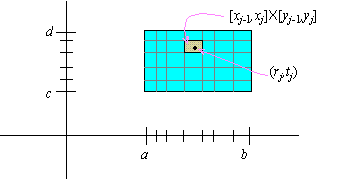
The Riemann sum of a function f( x,y) over this partition of [ a,b] ×[ c,d] is

[ a,b] ×[ c,d]     f( x,y)dA = lim h® 0  lim l®0  m å j = 1  n å k = 1  f( sj,tk) DxjDyk

To define the double integral over a bounded region R other than a rectangle, we choose a rectangle [ a,b] ×[ c,d] that contains R,

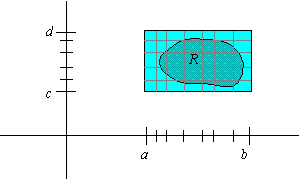
and we define g so that g( x,y) = f( x,y) if ( x,y) is in R and g( x,y) = 0 otherwise. The double integral of f( x,y) over an arbitrary region R is then defined to be

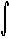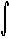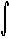f( x,y) dA = g( x,y) dA 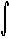R [ a,b] ×[c,d]

It then follows from the definition that the double integral satisfies the following properties:

R   [ f( x,y) +g( x,y) ] dA = R   f( x,y) dA + R   g( x,y) dA (1) R  [ f( x,y) -g( x,y) ] dA = R   f( x,y) dA-R   g( x,y) dA (2) R   kf( x,y) dA = kR   f( x,y) dA (3)

where k is a constant.      

EXAMPLE 1    Evaluate the integral of f+g over R if

R   f( x,y) dA= 3    and    R   g( x,y) dA = 2

(4)

Solution: We use property (1) to write

R   [ f( x,y) +g( x,y) ] dA = R   f( x,y) dA + R   g( x,y) dA = 3+2 = 5