Converting Double Integrals into Polar Coordinates
When the region of integration of a double integral is a circle or part of a circle, then it may be advantageous to convert the double integral to an iterated integral in polar coordinates. Also, if the integral involves expressions of the form
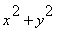 , then it may be advantageous to convert to polar coordinates. To do so, the region of integration must be described in polar coordinates, and then the area differential is replaced by
, then it may be advantageous to convert to polar coordinates. To do so, the region of integration must be described in polar coordinates, and then the area differential is replaced by
![]()
Let's look at an example:
Example:
Evaluate the following integral by transforming to polar coordinates:
![]()
To begin with, Maple cannot evaluate this iterated integral directly, as you will see below.
| > | Int_xy:=Int(Int(sqrt(x^2+y^2),y=-sqrt(1-x^2)..sqrt(1-x^2)),x=-1..1); value(%); |
| > |
Instead, Maple requires the conceptual assistance of a human to transform the iterated integral into a more natural representation in polar coordinates. To begin with, we must transform the region of integration into polar coordinates. We do so by noticing that the region
x =
-1..1 and
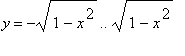 is the unit circle
is the unit circle
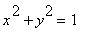 .
.
![[Maple Plot]](images/4-56.gif)
(commands for creating the figure above)
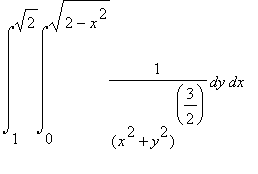
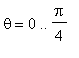 .
.
![[Maple Plot]](images/4-513.gif)