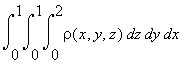| > |
xmin:=0:
xmax:=1:
ymin:=0:
ymax:=1:
ztop:=2:
zbot:=0:
n:=10: #total number of subintervals in x direction
m:=10: #total number of subintervals in y direction
r:=10: #total number of subintervals in z direction
x_subinterval:=5: #enter an integer between 1 and n
y_subinterval:=4: #enter an integer between 1 and m
z_subinterval:=5: #enter an integer between 1 and r
# Calculate point, box, surface
deltx:=(xmax-xmin)/n:
x_at := xmin+deltx*x_subinterval:
delty:=(ymax-ymin)/m:
y_at := ymin+delty*y_subinterval:
deltz:= abs(subs(x=x_at,y=y_at,ztop)-subs(x=x_at,y=y_at,zbot) )/r:
z_at := subs(x=x_at,y=y_at,zbot)+deltz*z_subinterval:
U_at:=subs(x=x_at-deltx/2,y=y_at-delty/2,z=z_at-deltz/2,U):
#surfaces
p1:=plot3d({ztop,zbot},x=xmin..xmax,y=ymin..ymax,
color=magenta,style=wireframe,axes=boxed,grid=[n+1,m+1]):
p2:=plot3d([xmin,y,v],y=ymin..ymax,v=subs(x=xmin,zbot)..subs(x=xmin,ztop),
color=blue,style=wireframe,grid=[m+1,r+1]):
p3:=plot3d([xmax,y,v],y=ymin..ymax,v=subs(x=xmax,zbot)..subs(x=xmax,ztop),
color=blue,style=wireframe,grid=[m+1,r+1]):
p4:=plot3d([x,ymin,v],x=xmin..xmax,v=subs(y=ymin,zbot)..subs(y=ymin,ztop),
color=green,style=wireframe,grid=[m+1,r+1]):
p5:=plot3d([x,ymax,v],x=xmin..xmax,v=subs(y=ymax,zbot)..subs(y=ymax,ztop),
color=green,style=wireframe,grid=[m+1,r+1]):
#singlebox
side1:=polygon([[x_at,y_at,z_at-deltz],[x_at,y_at,z_at],[x_at,y_at-delty,z_at],
[x_at,y_at-delty,z_at-deltz]],color=magenta):
side2:=polygon([[x_at-deltx,y_at,z_at-deltz],[x_at-deltx,y_at,z_at],
[x_at-deltx,y_at-delty,z_at],
[x_at-deltx,y_at-delty,z_at-deltz]],color=magenta):
side3:=polygon([[x_at,y_at,z_at-deltz],[x_at,y_at,z_at],[x_at-deltx,y_at,z_at],
[x_at-deltx,y_at,z_at-deltz]],color=magenta):
side4:=polygon([[x_at,y_at-delty,z_at-deltz],[x_at,y_at-delty,z_at], [x_at-deltx,y_at-delty,z_at],
[x_at-deltx,y_at-delty,z_at-deltz]],color=magenta):
atop:= polygon([[x_at,y_at,z_at],[x_at-deltx,y_at,z_at],[x_at-deltx,y_at-delty,z_at],
[x_at,y_at-delty,z_at]],color=magenta):
bot:= polygon([[x_at,y_at,z_at-deltz],[x_at-deltx,y_at,z_at-deltz],
[x_at-deltx,y_at-delty,z_at-deltz],
[x_at,y_at-delty,z_at-deltz]],color=magenta):
t1:=textplot3d([1.01*x_at,1.01*y_at,z_at-deltz/2,"dQ = rho(x,y,z)dxdydz"],color=black,
font=[TIMES,ROMAN,14],align=RIGHT):
display(side1,side2,side3,side4,atop,bot,p1,p2,p3,p4,p5,t1,pcloud,orientation=[-45,60]);
|
![[Maple Plot]](images/4-615.gif)
![Limit(sum(sum(sum(rho(s[j],t[k],u[l])*Delta*x[j]*Delta*y[k]*Delta*z[l],l = 1 .. r),k = 1 .. m),j = 1 .. n),h = 0)](images/4-619.gif) =
=