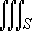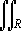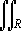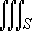Part 1: Definition of the Triple Integral

We can extend the concept of an integral into even higher dimensions. Indeed, in this section we develop the concept of a triple integral as an extension of the double integral definition.

To begin with, the notation [ a,b] ×[ c,d]×[ p,q] denotes the parallelepiped whose width, length, and height correspond to [ a,b] , [ c,d] , and [ p,q] , respectively, and let { x_j,t_j} , { y_k,u_k} , and { z_l,v_l} denote tagged partitions of those intervals, respectively,

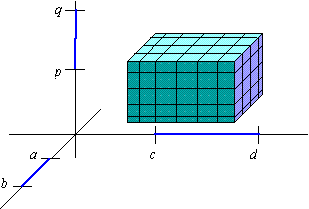
Given a function f( x,y,z) of 3 variables, its Riemann sum over this partition of the parallelepiped [ a,b] ×[c,d] ×[ p,q] is given by

For an arbitrary bounded solid S, we define g( x,y,z) = f( x,y,z) if ( x,y,z) is in S and we define g( x,y,z) = 0 otherwise. As a result, the solid is "approximated" by a collection of "small boxes" with volume Dx_j Dy_k Dz_l .

 
click to change the viewpoint

As a result, we can define the triple integral of f( x,y,z) over an arbitrary solid S by

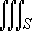f( x,y,z) dV = [ a,b] ×[ c,d] ×[ p,q] g( x,y,z) dV

where [ a,b] ×[ c,d] ×[ p,q] contains S.

For example, if f( x,y) ³ g( x,y) over a region R in the xy-plane, then the triple integral of f( x,y,z) over the solid S bound between two surfaces z = g( x,y) and z = f( x,y) over the region R is given by

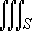f( x,y,z) dV = 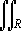é ë ó õ f( x,y) g(x,y)   f( x,y,z) dz ù û   dA

(1)

where dA is the area differential in the xy-plane.       

EXAMPLE 1    Compute the triple integral of f(x,y,z) = 8xyz over the solid between z = 0 and z = 1 and over the region

R: x = 0 y = 2 x = 1 y = 3

Solution: To do so, we use (1) to write

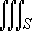8xyz  dV 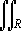=   ó õ 1 0  8xyz  dz    dA 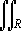=  4xyz2| 01   dA 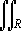= 4xy  dA

We then evaluate the resulting double integral over R:

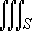8xyz  dV = ó õ 1 0  ó õ 3 2  4xy  dydx = 5

       

Likewise, if p( y,z) ³ q( y,z) over a region R in the yz-plane, then the triple integral of f(x,y,z) over the solid S bound between the two surfaces x = q(y,z) and x = p( y,z) over the region R is given by

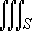f( x,y,z) dV = 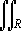é ë ó õ p( x,y) q(y,z)   f( x,y,z) dx ù û   dA1

where dA₁ is the area differential in the yz-plane. Moreover, if f( x,y,z) = 1, then the triple integral yields the volume of S

Volume  of  S =  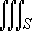dV

EXAMPLE 2    What is the volume of the solid between x = yz and x = 0 over the region y = 0, y = 1, z = 0, z = 4.       

Solution: The volume is given by

V =  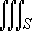dV = 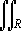ó õ yz 0  dx  dA1

Indeed, substituting the boundaries for R leads to the triple iterated integral

V = ó õ 4 0  ó õ 1 0  ó õ yz 0  dxdydz

Evaluating each integral in succession then leads to

V = ó õ 4 0  ó õ 1 0  yz  dydz = ó õ 4 0  z  y2 2 ê ê y = 1 y = 0  dz = ó õ 4 0   z 2 dz = 4