Part 4: Moments and Centers of Mass

If a solid S has a mass density of m( x,y,z) , then its first moments are defined to be

Myz =   xm( x,y,z) dV,    Mxz =  ym( x,y,z) dV

Mxy =   zm( x,y,z) dV

Since the mass of S is given by

M =  m( x,y,z) dV

the moments allow us to generalize the concept of center of mass to arbitrary solids. In particular, the center of mass of a solid with mass density m( x,y,z) is defined to be the point in R³ with coordinates

x  =   Myz M ,    y  =   Mxz M ,    z  =   Mxy M

EXAMPLE 7    Find the center of mass of the rectangular bar [ 0,1] ×[ 0,1] ×[ 0,3] when the mass density is given by

r( x,y,z) = 4-y    kg  per  meter

Solution: The mass of the box is

M =  ( 4-y) dV

The triple integral easily reduces to a system of 3 iterated integrals

M = 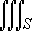ó õ 1 0  ó õ 3 0  ó õ 1 0  ( 4-y) dzdydx = 7.5  kg

The remaining integrals are given by

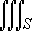
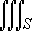
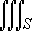
Myz = x  r( x,y,z)dV = ó õ 1 0  ó õ 3 0  ó õ 1 0  ( 4-y) x dzdydx Mxz = y  r( x,y,z)dV = ó õ 1 0  ó õ 3 0  ó õ 1 0  ( 4-y) y dzdydx Mxy = z  r( x,y,z)dV = ó õ 1 0  ó õ 3 0  ó õ 1 0  ( 4-y) z dzdydx

Evaluating these integrals and computing the coordinates of the center of mass yields

Myz = 3.75  kg-m,        x  =   3. 75 7.5 = 0.5  m Mxz = 9  kg-m,        y  =   9 7.5 = 1.2  m Mxy = 3.75  kg-m,        z  =   3. 75 7.5 = 0.5  m

Thus, the center of mass is ( 0.5,1.2,0.5) .