Densities in Spherical Coordinates
Spheres occur frequently in applications, and as a result, questions involving densities for spheres are commonplace. For example, let's consider the charge density given by
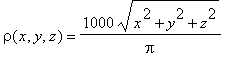
Below we have distributed 1,000 "charges" in a sphere of radius 1 meter based on this density.
![[Maple Plot]](images/4-713.gif)
(commands used to generate figure above)
In cartesian coordinates, the total charge is given by 3 iterated integrals:
| > |
Q:=Int(Int(Int(1000/Pi*sqrt(x^2+y^2+z^2),z=-sqrt(1-x^2-y^2)..sqrt(1-x^2-y^2)),y=-sqrt(1-x^2)..sqrt(1-x^2)),x=-1..1);
value(%);
|
In cartesian coordinates, Maple is unable to evaluate the integral. However, in spherical coordinates, the triple integral would instead result in
| > |
Q:=Int(Int(Int((1000/Pi*rho)*rho^2*sin(phi),rho=0..1),phi=0..Pi),theta=0..2*Pi);
Q:=value(%);
|
Let's look at another example. Let's consider a solid sphere with a uniform mass density of
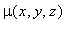 = 5
= 5
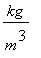 . If we assume that each small "chunk" of a solid with mass
dM
exerts a small amount of potential
dU
, then the inverse square field potential on an object at (0,0,3) due to the "chunk" is given by
. If we assume that each small "chunk" of a solid with mass
dM
exerts a small amount of potential
dU
, then the inverse square field potential on an object at (0,0,3) due to the "chunk" is given by
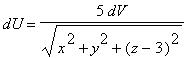
Let's convert this into spherical coordinates and then integrate to find the total potential acting on an object at (0,0,2).
To begin with, let's define
dU
in cartesian coordinates.
| > |
dU:=5*dV/sqrt(x^2+y^2+(z-3)^2);
|
Next, let's convert the integrand into spherical coordinates by substituting for
x, y
, and
z
:
Also, we let
dV
=
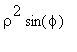 since the differentials will be handled by the
Int
command.
since the differentials will be handled by the
Int
command.
| > |
dU:=subs(x=rho*sin(phi)*cos(theta),y=rho*sin(phi)*sin(theta),z=rho*cos(phi),dV=rho^2*sin(phi),dU);
dU:=simplify(%);
|
Now let's integrate
dU
over the sphere to find the total potential
U.
| > |
U:=Int(Int(Int(dU,rho=0..1),phi=0..Pi),theta=0..2*Pi);
U:=value(%);
|
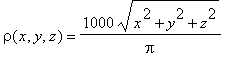
![[Maple Plot]](images/4-713.gif)
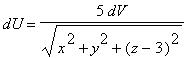
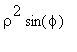 since the differentials will be handled by the
Int
command.
since the differentials will be handled by the
Int
command.