Pullbacks into Polar Coordinates   

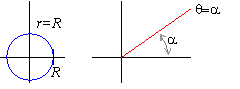
If we are given a curve in the xy-plane, then the identities x = rcos( q) and x = rsin( q) can be used to pull the curve back into polar coordinates. For example, x²+y² = R² is pulled back into polar coordinates by substituting x = rcos( q) and x = rsin( q) :

x2+y2 = R2    Þ     r2cos2( q) +r2sin2( q) = R2    Þ    r2 = R2

which implies r = R. That is, if R is constant, then r = R is a circle centered at the origin in the xy-plane.

Similarly, lines of the form y = mx become

rsin( q) = mrcos( q)    Þ     sin( q) = mcos( q)     Þ     tan( q) = m

Thus, if a = tan^-1( m) is constant, then q = a is the ray beginning at the origin.

In general, the pullback into polar coordinates of a curve in xy-coordinates is the result of substituting x = rcos( q) and x = rsin( q) into the equation of the curve and simplifying. The identity x²+y² = r² is also often used in converting the xy-equation of a curve into polar coordinates.

       

EXAMPLE 6    Convert the curve x²+y² = 2x into polar coordinates.       

Solution: To do so, we replace x²+y² by r² and let x = rcos( q) :

r2 = 2rcos( q)

Solving for r then yields

r = 2cos( q)

       

The curve x²+y² = 2x, and correspondingly its pullback r = 2cos( q) into polar coordinates, is a circle of radius 1 centered at ( 1,0) . In general, a curve of the form r = 2acos( q) is a circle of radius | a| centered at ( a,0) and a curve of the form r = 2asin(q) is a circle of radius | a| centered at (0, a) .

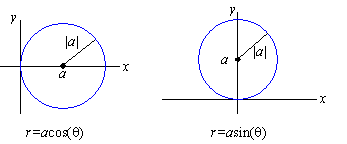
Let's look at another example.

EXAMPLE 7    Find the pullback of   y = 2x+1 into polar coordinates.       

Solution: To do so, we let x = r cos(q) and we let y = r sin(q) :

r sin(q)  =   2r cos( q) + 1 r sin(q) - 2r cos(q)  = 1

Solving for r then yields

r =   1 sin(q) - 2cos(q)