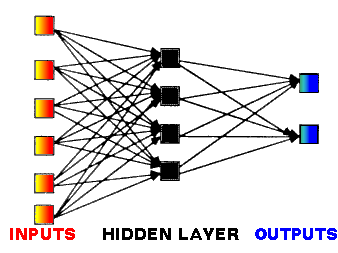
Artificial Neurons
An artificial neuron is a component in an Artificial Neural Network
(ANN) which has both an internal "state" variable sj and an output
variable xj.
The connections between the individual artificial neurons have weights $
\omega _{ij}$, and the state variable $s_{j}$ is subsequently given by
\[
s_{j}=\sum_{i=0,\ i\neq j}^{n}\omega _{ij}x_{j}
\]
The $j^{th}$ output variable is then defined to be
\[
x_{j}=\sigma \left( s_{j}\right)
\]
where $\sigma $ is a sigmoidal activation function. Thus, the
network is a collection of sum-and-fire components.
Common choices for $\sigma $ are the discrete firing function
\[
\sigma \left( s_{j}-\theta _{j}\right) =\left\{
\begin{array}{c}
1\ if\ s_{j}>\theta _{j} \\
0\ if\ s_{j}\leq \theta _{j}
\end{array}
\right.
\]
where $\theta _{j}$ is the threshold for the the neuron; and also,
\[
\sigma \left( s_{j}-\theta _{j}\right) =\frac{1}{1+e^{-\left( s_{j}-\theta
_{j}\right) }}
\]
which is shown below: