Electric Cables
The mathematical model of a neuron begins with the assumption that the
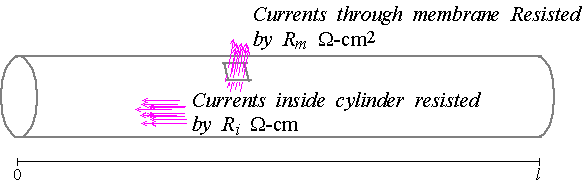
dendrites and axon of a neuron can be modeled by cables, where a cable is a
cylinder with length $l$ and radius $a$ which is considered to have a
continuous distribution of internal and membrane resistances. However, we
will instead begin with the concept of conductance, which is the
multiplicative inverse of resistance and which is a measure of the ease with
which currents flow through a region.
Specifically, a cross-section of the cable at $x$ units along the length of
the cable from its beginning is a disk with radius $a.$ The conductance
through this disk is $\pi a^{2}G_{i}\left( x\right),$ where
$G_{i}\left(x\right) $ is the specific conductance per unit area through the
disk. The specific conductance $G_{i}\left( x\right) $ is actually a
density, which is to say that it is the conductance per unit length of the
cylinder -- i.e., in units of siemans per centimeter. Thus, the resistance
through the disk is the multiplicative inverse
\[
\frac{1}{\pi a^{2}G_{i}\left( x\right) }=\frac{R_{i}\left( x\right) }{\pi
a^{2}}
\]
where $R_{i}\left( x\right) =1/G_{i}\left( x\right) $ is the specific
resistance of the disk in units of ohms-centimeters ($\Omega $~$cm$ ).
Similarly, we define $G_{m}\left( x\right)$ to be the specific membrane
conductance for currents through the boundary surface of the cylinder
(i.e., the "membrane") in units of
siemens per unit area; and we define $C_{m}\left( x\right) $ to be the
specific membrane capacitance, in units of Farads per unit area. The
specific membrane resistance is thus $R_{m}\left( x\right) =1/G_{m}\left(
x\right) $ in units of $\Omega ~cm^{2}$. Thus, $R_{i}\left( x\right) $ and
$R_{m}\left( x\right) $ can be interpreted as resistances through small
"patches" of the internal cytoplasm and surrounding membrane, respectively.
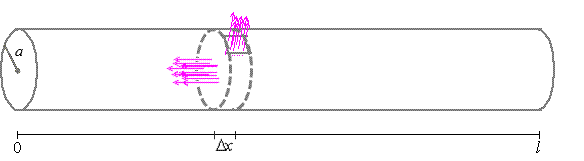
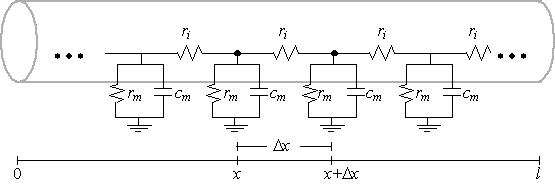
Empirical studies allow us to assume uniform cross-sections, so that the
voltage drop across the membrane can be approximated by a
ladder circuit, which is a sequence of parallel RC-circuits. To do so, we define
$r_{i}$ to be the resistance through a short cylindrical cross-section
between $x$ and $x+\Delta x$ centimeters along the length of the cable with
width $\Delta x\approx 0$ and a radius of $a$.
Assuming each disk between
$x$ and $x+\Delta x$ has the same resistance
$\frac{R_{i}\left( x\right) }{\pi a^{2}},$
the total resistance through the cylindrical cross-section is
\[
r_{i}=\frac{R_{i}\left( x\right) }{\pi a^{2}} \Delta x
\]
The membrane conductance for the intersection of the cable and the short
cylindrical cross-section is
\[
g_{m}=G_{m}\left( x\right) \Delta x
\]
which means the ladder circuit requires a membrane resistance at each
point of
\[
r_{m}=\frac{1}{g_{m}}=\frac{R_{m}\left( x\right) }{2\pi a\Delta x}
\]
and a capacitance of $c_{m}=2\pi aC_{m}\left( x\right) \Delta x.$
Let's use the ideas above to develop the cable equation for the propagation
of electricity through a cable. If we let $V(x,t)$ denote the membrane
voltage at $x$ units from the origin and at time $t$, then between $x$ and $
x+\Delta x$ there is an axial current $I_{axial}$ through the resistor $r_{i}
$ for the interval $\left[ x,x+\Delta x\right] .$ This current is due to the
difference in the voltages $V(x,t)$ and $V(x+\Delta x,t)$.
Ohm's law thus implies that
\[
V\left( x+\Delta x\right) -V\left( x\right) =-r_{i}I_{axial}
\]
since positive current flow is toward the beginning of the cylinder. Since $
r_{i}=R_{i}\left( x\right) \Delta x/\left( \pi a^{2}\right) $, this leads to
\[
V\left( x+\Delta x\right) -V\left( x\right) =-\frac{R_{i}\left( x\right) }{
\pi a^{2}} \Delta x I_{axial}
\]
Solving for the axial current then leads to
\[
I_{axial}=\frac{-\pi a^{2}}{R_{i}\left( x\right) } \frac{V\left( x+\Delta
x\right) -V\left( x\right) }{\Delta x}\rightarrow \frac{-\pi a^{2}}{
R_{i}\left( x\right) }\frac{\partial V}{\partial x}
\]
That is, the ladder approximations become exact in the limit as $\Delta x$ approaches
0, or correspondingly, as the number of parallel RC circuits per unit length
goes to infinity.
Any loss in the axial current must be due to the propogation of currents
through the membrane (or to "leakage"
which we ignore for now). That is,
\[
-\Delta I_{axial}=I_{m}
\]
where $I_{m}$ represents the amount of current through the membrane. There
are three sources of current through the membrane. First, there is current
$I_{z}$, which via Ohm's law satisfies $V=r_{m}I_{z}$ (or equivalently,
$I_{z}=V/r_{m}$ ). Second, there is current across the membrane
capacitance, which is
\[
I_{c}=c_{m}\frac{\partial V}{\partial t}
\]
and finally, there is a chemically induced ionic current density $I_{ion}$
amps per unit length, so that $I_{ion}\Delta x$ is the actual change in
current. Altogether, this means that
\[
-\Delta I_{axial}=I_{z}+I_{c}+I_{ion}\Delta x
\]
which upon substitution leads to
\[
-\Delta I_{axial}=\frac{V}{r_{m}}+c_{m}\frac{\partial V}{\partial t}
+I_{ion}\Delta x
\]
Since $r_{m}=R_{m}\left( x\right) /\left( 2\pi a\Delta x\right) $ and
$c_{m}=2\pi aC_{m}\left( x\right) \Delta x,$ this leads to
\[
-\Delta I_{axial}=\frac{V}{R_{m}\left( x\right) /\left( 2\pi a\Delta
x\right) }+2\pi aC_{m}\left( x\right) \Delta x\frac{\partial V}{\partial t}
+I_{ion}\Delta x
\]
so that
\[
\frac{-1}{2\pi a}\frac{\Delta I_{axial}}{\Delta x}=\frac{V}{R_{m}\left(
x\right) }+C_{m}\left( x\right) \frac{\partial V}{\partial t}+I_{ion}
\]
In the limit as $\Delta x\rightarrow 0,$ the result is the
cable equation, which is
\[
\frac{a}{2}\frac{\partial }{\partial x}\left( \frac{1}{R_{i}\left( x\right) }
\frac{\partial V}{\partial x}\right) =\frac{V}{R_{m}\left( x\right) }
+C_{m}\left( x\right) \frac{\partial V}{\partial t}+I_{ion}
\]
Typically, $R_{i}\left( x\right) $ is assumed to be constant (cytoplasm is
homogenous and uniform), so that we get
\[
\frac{aR_{m}\left( x\right) }{2R_{i}} \frac{\partial ^{2}V}{\partial x^{2}}
=R_{m}\left( x\right) C_{m}\left( x\right) \frac{\partial V}{\partial t}
+V+R_{m}\left( x\right) I_{ion}
\]
If we let $\tau _{m}\left( x\right) =r_{m}c_{m}=R_{m}\left( x\right)
C_{m}\left( x\right) $ be the membrane time constant, then
\[
\frac{aR_{m}\left( x\right) }{2R_{i}} \frac{\partial ^{2}V}{\partial x^{2}}
-\tau _{m}\left( x\right) \frac{\partial V}{\partial t}-V=R_{m}\left(
x\right) I_{ion}
\]
Alternately, we also usually assume that $C_{m}\left( x\right) $ is
constant, so that if we let
\[
t=C_{m}\left( x\right) T\quad and\quad x=\sqrt{\frac{a}{2R_{i}}}X
\]
then we obtain the membrane resistance form of the cable equation,
\[
R_{m}\left( X\right) \frac{\partial ^{2}V}{\partial X^{2}}-R_{m}\left(
X\right) \frac{\partial V}{\partial T}-V=R_{m}\left( X\right) I_{ion}
\]
for simplicity, this is often rewritten in terms of conductances as
\[
\frac{\partial ^{2}V}{\partial X^{2}}-\frac{\partial V}{\partial T}
-G_{m}\left( X\right) V=I_{ion}
\]
It is this last form that we will use later in the presentation.