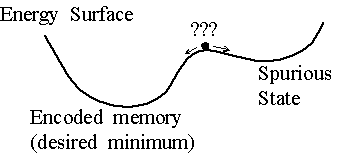
Energy
The energy of a Hopfield network is given by
\[
E=\frac{-1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\omega
_{ij}x_{i}x_{j}+\sum_{i=1}^{n}\theta _{i}x_{i}
\]
Suppose now that an $r^{th}$ neuron is chosen at random. Let $E^{old}$
denote the energy before the $r^{th}$ neuron "sums and
fires" and let $E^{new}$ denote the energy after. Then
because only the $r^{th}$ neuron actually changes, we have
\[
E^{new}=E^{old}-\frac{1}{2}\sum_{j=1}^{n}\omega _{rj}\left(
x_{r}^{new}-x_{r}^{old}\right) x_{j}-\frac{1}{2}\sum_{i=1}^{n}\omega
_{ir}x_{i}\left( x_{r}^{new}-x_{r}^{old}\right) +\theta _{r}\left(
x_{r}^{new}-x_{r}^{old}\right)
\]
Factoring out the common term yields
\begin{eqnarray*}
E^{new} &=&E^{old}-\left( \frac{1}{2}\sum_{j=1}^{n}\omega _{rj}x_{j}+\frac{1
}{2}\sum_{i=1}^{n}\omega _{ir}x_{i}-\theta _{r}\right) \left(
x_{r}^{new}-x_{r}^{old}\right) \\
&=&E^{old}-\left( \frac{1}{2}\left( \sum_{j=1}^{n}\left( \omega _{rj}+\omega
_{jr}\right) x_{j}\right) -\theta _{r}\right) \left(
x_{r}^{new}-x_{r}^{old}\right)
\end{eqnarray*}
Because of symmetry, we have
\[
E^{new}=E^{old}-\left( \sum_{j=1}^{n}\omega _{rj}x_{j}-\theta _{r}\right)
\left( x_{r}^{new}-x_{r}^{old}\right)
\]
If $x_{r}^{new}-x_{r}^{old}\geq 0,$ then the neuron must have fired,
implying that
\[
\sum_{j=1}^{n}\omega _{rj}x_{j}>\theta _{r}\quad and\quad \left(
\sum_{j=1}^{n}\omega _{rj}x_{j}-\theta _{r}\right) \left(
x_{r}^{new}-x_{r}^{old}\right) \geq 0
\]
If $x_{r}^{new}-x_{r}^{old}\leq 0,$then the neuron did not fire, which
implies that
\[
\sum_{j=1}^{n}\omega _{rj}x_{j}\leq \theta _{r}\quad and\quad \left(
\sum_{j=1}^{n}\omega _{rj}x_{j}-\theta _{r}\right) \left(
x_{r}^{new}-x_{r}^{old}\right) \geq 0
\]
Either way, $E^{new}\leq E^{old}$
Thus, if firing is performed at random, then the error always decreases. As
a result, we can conclude that a neural network converges to a state
that makes E a minimum. Fortunately, Hebbian learning encodes new
information into minima of the energy function. However, Hebbian learning
also leads to undesirable local minima which are known as spurious
states..