

The purpose of this lab is to give you an opportunity to design chip selects. I realize that the lecture did not go smoothly for everyone, so hopefully this lab will compensate.
I have designed a LabView virtual instrument that takes a hexadecimal number and breaks it into its individual bits. This program should be stored in each of your computers at C:\CSCI2150\Chipsel.vi. The front panel to this VI is shown below.
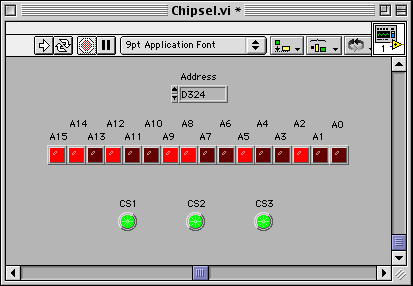
The address input is the sole input of the panel. In it, you can input a value from 000016 to FFFF16. The row of LEDs labeled A0, A1, A2, ... A15 represent the individual bits of the hexadecimal number. You will notice that the number D32416 is displayed which results in the binary value 1101 0011 0010 01002 that is displayed on the LEDs.
In addition, you will notice that there are three LEDs at the bottom of the panel labeled CS1, CS2, and CS3. These are the outputs that you are going to create the software for.
As for the diagram, you get the little bit of wiring I did to break the hex value into bits, the individual bits A0 through A15 that you will use to create the chip selects, and the chip select outputs CS1, CS2, and CS3. The diagram is shown below.
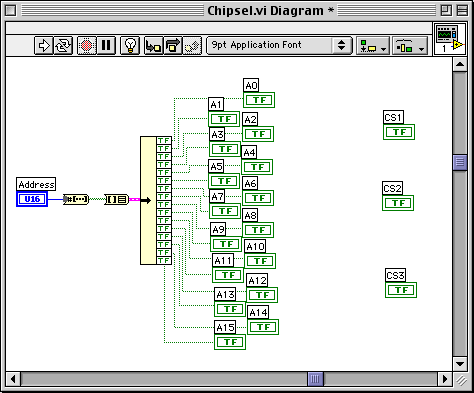
Your job, plain and simple, will be to design the logic for the three chip selects so that the memory range for each chip select is equal to that shown below.
| Chip Select | Low Address | High Address |
| CS1 | 000016 | 3FFF16 |
| CS2 | 800016 | 87FF16 |
| CS3 | C00016 | CFFF16 |
Once you've designed the chip selects, you will be able to test them using the LabView virtual instrument.
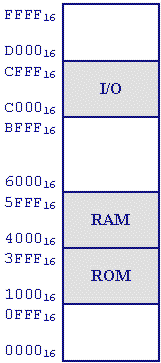
The need for memory mapping (assigning different components of memory to different portions of the memory map) arises from the need to have multiple memory devices accessible across a single address/data bus. Therefore, we need to have a method of setting the "base" or "starting" address of a memory device to an address other than 0. For example, the memory map below has a ROM starting at address 0x1000, a RAM starting at 0x4000, and a piece of memory-mapped I/O starting at address 0xC000.
Let's start by reviewing the basic structure of a memory chip. The figure below shows the basic components of a memory chip.
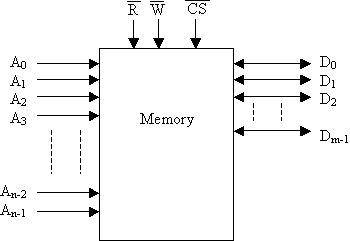
It has n input address lines, therefore, the size of the memory is 2n. It has m data lines, and therefore can store m bits of data for each address. The main lines of control for the memory are ^R, ^W, and ^CS. When ^R is low, the processor is reading from the memory and the memory should be outputting data on its data lines. When ^W is low, then the processor is writing data and the memory should be inputting data to store in the memory cells.
If ^CS is high, the data lines of the chip are disabled. It is as if the chip is not even connected. When ^CS is low, the data lines are enabled for input or output based on the state of ^R and ^W. It is this ^CS line that enables multiple devices to be connected to a single set of data lines as shown in the image below.

As far as the processor is concerned, it has n output address lines where this n must be at least as large and most likely larger than the n input address lines to the memory chip. In this case, n gives you the size of your memory space (the number of memory locations addressable by the processor) and is once again calculated as 2n. It also has m labeled D0 through Dm-1 where m is the number of bits of data. This m should be the same value as the m on the memory chips.
Assume we have a 1 Meg address space. (I.e., the processor can address up to 1,048,576 memory spaces.) How many address lines does the processor have?
220 = 1,048,576
Therefore, the processor has 20 output address lines
Assume we want to insert a 64K (65,536 memory addresses) RAM starting at address 0x48000. First, how many address lines does the 64K memory chip have?
216 = 65,536
Therefore, the memory has 16 input address lines
First, convert the hexadecimal low address of 0x48000 to binary.
| Hexadecimal | 4 | 8 | 0 | 0 | 0 |
| Binary | 0100 | 1000 | 0000 | 0000 | 0000 |
Now, divide the processor's address lines into the addresses that will be input to the memory and the addresses that will be used to create the chip select.
| A19 | A18 | A17 | A16 | A15 | A14 | A13 | A12 | A11 | A10 | A9 | A8 | A7 | A6 | A5 | A4 | A3 | A2 | A1 | A0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| The chip select will use these 4 lines |
These 16 address lines must go to memory chip |
||||||||||||||||||
Okay, so we have a problem. A15 is a one for the lowest address, but since it is one of the address lines to the memory chip, its low address value MUST BE A ZERO.
Therefore, the low address of the 64K memory chip must either be incremented so that it goes to the next address where A0 through A15 all equal zeros or decremented to the first address below 0x48000 where A0 through A15 all equal zeros. These two options are shown below.
| A19 | A18 | A17 | A16 | A15 | A14 | A13 | A12 | A11 | A10 | A9 | A8 | A7 | A6 | A5 | A4 | A3 | A2 | A1 | A0 | |
| Next highest | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Next lowest | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Let's pick the next highest address, binary 0101 0000 0000 0000 0000 which equals 0x50000 in hexadecimal. What will be the 64K memory's highest address? Well, it will be the address where all of the address lines, A0 through A15, are one. That value is binary 0101 1111 1111 1111 1111 which equals 0x5FFFF in hexadecimal. The resulting memory map is shown below.
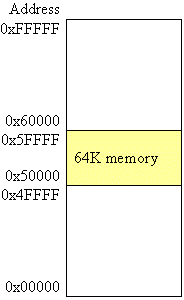
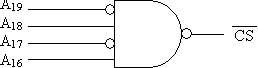
We now need to make a chip select that is a logic zero only when A19 = 0, A18 = 1, A17 = 0, and A16 = 1. Using a NAND gate as we have in class for the 1-of-x selectors, we get:
Now let's get back to designing the chip selects for this lab. I want you do to five things:
Once you have finished your LabView circuits, call me over to verify their operation.
Happy programming!
Developed by David Tarnoff for the Spring 2001 sections of CSCI 2150 at ETSU