Although the set of notes you have requested is presented below, it has not been maintained since January, 2003. All of the information in these notes has been included in an on-line text titled Computer Organization and Design Fundamentals. The book is available in three formats, two of which are free electronic downloads. Please visit one of the following links in order to access the format you prefer.
Thank you for your interest in this textbook. Please feel free to e-mail me at tarnoff etsu.edu if you have any questions or comments.
-Dave Tarnoff
Reading: Floyd, Sections 2.7 through 2.8 and 3.1 through 3.6
It made some of you nervous during our discussion of adding 2's complement values that sometimes we disregarded a carry. This is not always the case. Sometimes, a carry is an indication that an error occurred. If we add two n-bit binary numbers using 2's complement notation, the result must fall between the minimum and maximum values identified by the following equations.
Minimum 2's complement value = -2n-1
Maximum 2's complement value = 2n-1 - 1
This doesn't always happen. When a result falls outside the valid range, we call this an overflow.
But how can the computer determine if an overflow occurred? It simply examines the sign bit (MSB) of both numbers being added and the sign bit of the result.
If the sign bits of both numbers being added are different, i.e., one number is positive and one number is negative, no overflow can occur. If the sign bits of both numbers being added are the same, i.e., both numbers are positive or both numbers are negative, then the sign bits must be compared to the sign bit of the result. If the sign bit of the result is different, i.e., the addition of two positive numbers resulted in a negative number or the addition of two negative numbers resulted in a positive number, we've had an overflow. Below is an example where the addition of two 8-bit positive numbers results in a negative value.
2's compl. Decimal10011000 -104
|
If this had been done assuming unsigned notation, the result of 152 would have been fine. 152 is, however, outside the range of 2's complement representation using 8 bits.
As far as human recognition of binary numbers goes, our performance is poor. Unless you are quite experienced at using binary numbers, recognizing the relative magnitudes of 101011012 and 101001012 is not immediate (173 is greater than 165). Nor is it immediately apparent to us that 10011011012 equals 62110 without going through the process of calculating 512 + 64 + 32 + 8 + 4 + 1.
To make the binary representation of numbers easier on us humans, there is a shorthand representation for binary values. It begins by partitioning a binary number into its nibbles (4-bit groups) starting at the LSB. An example is shown below:
| The number: | 1001011110110100100111 |
|||||
| ...can be divided into: | 10 |
0101 |
1110 |
1101 |
0010 |
0111 |
Next, a symbol is used to represent each of the possible combinations of bits in a nibble. We start by numbering them with values equivalent to their binary value, i.e.:
| 00002 = 010 |
| 00012 = 110 |
| 00102 = 210 |
| : : : |
| 10002 = 810 |
| 10012 = 910 |
At 9, we run out of decimal characters. There are six more nibbles to label, so we begin using letters: A, B, C, D, E, and F. These represent the decimal values 10, 11, 12, 13, 14, and 15 respectively.
| 10102 = A |
| 10112 = B |
| : : : |
| 11112 = F |
This gives us the hexadecimal sequence of digits.
| Decimal | Binary | Hexadecimal |
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
Another way to look at it is that hexadecimal (hex) counting is also similar to decimal except that instead of having 10 numerals, it has sixteen.
Now how do we convert binary to decimal? Simply divide the binary number into its nibbles (if the number of bits is not divisible by 4, add leading zeros), then nibble-by-nibble use the table above to find the hexadecimal equivalent to each nibble. For example:
| The number: | 1001011110110100100111 |
|||||
| ...is divided into: | 0010 |
0101 |
1110 |
1101 |
0010 |
0111 |
| ...which translates to: | 2 |
5 |
E |
D |
2 |
7 |
Therefore, 10010111101101001001112 = 25ED2716.
Going the other way is just as easy. Translating 5D3F2116 to binary goes something like this:
| The hexadecimal value: | 5 |
D |
3 |
F |
2 |
1 |
| ...translates to: | 0101 |
1101 |
0011 |
1111 |
0010 |
0001 |
Therefore, 5D3F2116 = 0101110100111111001000012.
In an effort to afford decimal notation the same convenience of conversion to binary that hex has, Binary Coded Decimal (BCD) was developed. The only reason it is introduced here is to make you aware of BCD if you see it used in assembly language.
As in hex, each decimal digit represents a nibble of the binary equivalent. The table below shows the conversion between each decimal digit and the binary equivalent.
|
|
For example, the following converts the BCD value 1 0110 1001 0010 to decimal
| The BCD value: | 0001 |
0110 |
1001 |
0010 |
| ...has the decimal value: | 1 |
6 |
9 |
2 |
It is important to note that there is no numerical conversion between BCD and decimal. BCD is only a way to represent decimal numbers in binary.
Another item of note is that not all binary numbers convert from BCD to decimal. 0101 1011 0101 for example is an illegal BCD value because the middle nibble is illegal.
When two BCD numbers are added, the digits 1010, 1011, 1100, 1101, 1110, and 1111 must be avoided. This is done by adding an additional step anytime the binary addition of two nibbles results in one of these values or a carry. If this occurs, simply add an additional 6 to skip over the invalid values. For example:
BCD Decimal1011 Invalid
|
This step is also necessary if a carry results from a BCD addition.
BCD Decimal10001 Carry
|
Individually, logic gates are not very practical. Their power comes when you combine them to create a digital circuit.

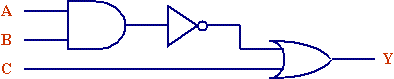
At this point, you can determine the truth table by examining the circuit for each possible combination of inputs. For example, A=1, B=0, and C=0 produces the following output:
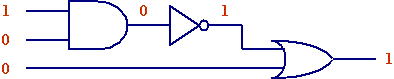
The 1/0 input to the AND gate produces a 0 output. (Remember there's only a 1 output if all the inputs are 1 for the AND gate.) The inverter flips the value from a 0 to a 1. That makes an input of 1/0 for the OR gate resulting in a 1 output. (Remember there's a 1 output from an OR gate if any of the inputs are 1.) Therefore, we have determined the output of the combinational logic circuit for one of the eight possible combinations of inputs. This procedure can be used for all 8 combinations of inputs to this circuit to determine the full truth table.
| Inputs | Outputs | ||
| A | B | C | Y |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Up to now, we have been using these gates in the static representation, i.e., truth tables. In many cases, we want to view the operation of combinational logic with reference to time as its inputs change. For example, assume the three waveforms of the figure below are input to a 3-input AND gate.
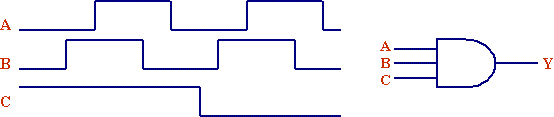
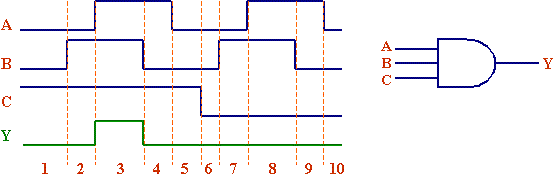
Determining the output waveform for this timing diagram is the same as determining the output of each row of a truth table. First, determine where the changes in the inputs occur.

Note that the dashed lines indicate where one or more of the inputs toggle. The periods of time between the dashed lines have constant inputs. Therefore, the only time when the output can change is when one of the inputs changes, i.e., at the dashed lines. Between the dashed lines, the output remains constant.
As for our example, the only time an AND gate has an output of logic 1 is when all of its inputs are logic 1. The only time this occurs in the figure is for the third section. Therefore, the output timing diagram is as shown below.
Copyright 2001 by David L. Tarnoff. All rights reserved.