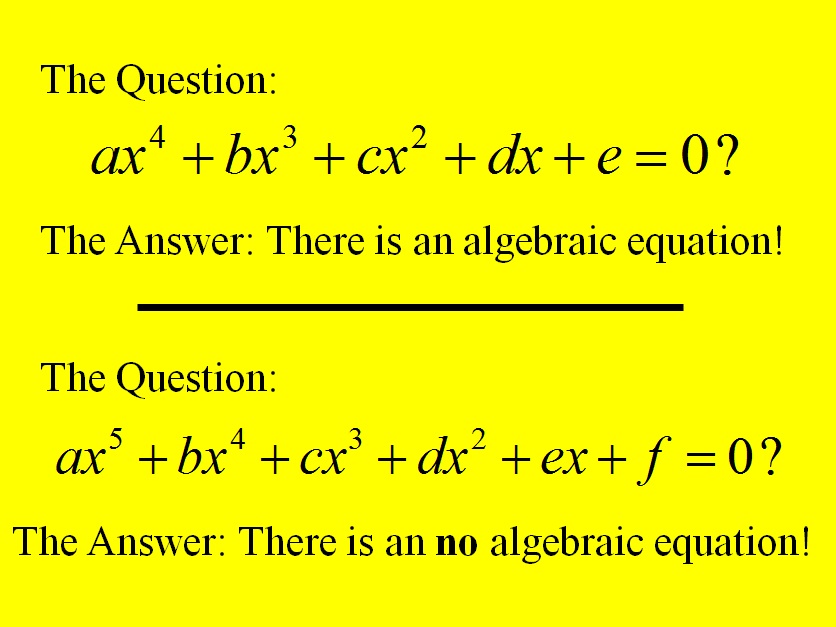The Bicentennial of Evariste Galois
Bob Gardner
East Tennessee State University
Department of Mathematics and Statistics
Johnson City, TN 37614
The Equation
In modern notation, this presentation is about expressing the solutions of the equation:
cnxn + cn-1xn-1 + cn-2xn-1 + . . . + c3x3+ c2x2+ c1x + c0
in an algebraic way. That is, what does x equal? Express the answer as a combination of the coefficients using the operations of addition, subtraction, multiplication, division, and extraction of roots. An algebraic solution is also sometimes called "solving by radicals."
A Familiar Example
A familiar example of the problem is to find the roots (or zeros) of the second degree equation
ax2+ bx + c = 0.
We want the values of x expressed in terms of a, b, and c and only with the use of addition, subtraction, multiplication, division, and the extraction of roots. Of course, the values of x are given by the familiar quadratic equation:
An Unfamiliar Example
Another example, which is likely not so familiar to you, is that of finding the values of x which result from setting a third degree polynomial equal to zero:
ax3+ bx2 + cx + d = 0.
Again, the values of x must be expressed in terms of the coefficients a, b, c, and d by using the algebraic operations. The reason you probably have not seen this in the past is that it is actually rather impractical and complicated.
Here are the solutions.
Notice that x2 and x3 involve square roots of negatives.
Fourth Degree and Fifth Degree Equations
There is a similar algebraic equation for the four solutions of the equation which results from setting a fourth degree polynomial equal to zero. However, there is no such algebraic equation for the solutions of a fifth degree polynomial set equal to zero.
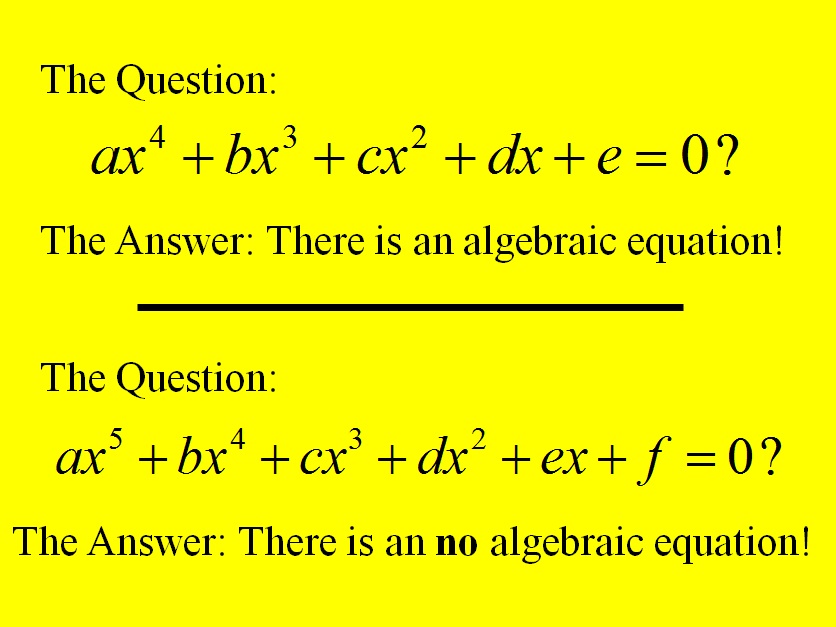This talk is a historical exploration of a key figure related to this second result.
Go to the next section: A Brief History of Equations.
Last revised October 19, 2011.
