4. 3-Manifolds

Lets describe the 3-sphere, S3. One way to think of it is to describe it by the equation

x12 + x22 + x32 + x42 = r2.
That is, the 3-sphere is the collection of all points (x1, x2, x3, x4) in 4-dimensional Euclidean space which statisfy this equation. However, this description relies on the 3-sphere being embedded in a higher dimensional space. This is no good for us since we are limited to discussing intrinsic properties. Lets describe what you would see as an inhabitant of a 3-sphere (this description is due to Thurston (1997, p. 32)). If you are the sole inhabitant of such a space, then you would see yourself in every direction you look. Suppose the circumference of this 3-sphere is C and suppose I am in this space with you. If I start to fly away from you, then you see my image get smaller and smaller until I am a distance of C/4 from you. Then my image starts to get larger. When I am only 3 feet from the point antipodal to you (which lies a distance C/2 from you), then I appear the same as I would when I am only 3 feet from you. When I arrive at the antipodal point, you see my image fill the entire sky! As with the case for the 2-sphere, these properties reveal that you are living in a 3-sphere. Again, you would discover that the geometry is elliptical. Georg Riemann first proposed that this model (also called the hypersphere) could represent the shape of our universe. Albert Einstein also favored this model in his early work on cosmology (see Luminet et al. 1999).

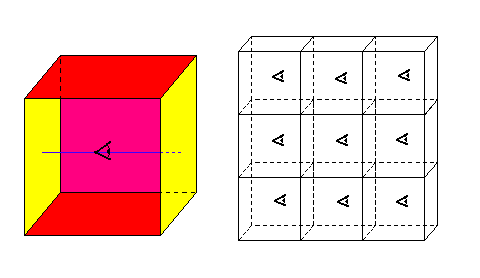
Now lets describe the view from inside of a flat 3-torus, T3. We start with a cube as the fundamental domain. "Conceptually" join the front and back of the cube, the left and the right, and the top and the bottom. In such a manifold, you will see yourself in six "fundamental" directions. In fact, you will see the sky filled with a grid of images of yourself! See Figure 8. To further illustrate the topology, suppose that I am in this space with you and that I fly away off to your left. You will see me fly towards the image of you which is to your left and nearest to you. At the same time, if you look to your right, you will see me leave the image of you which is to your right and nearest you. I will fly in towards you from the right. There are not "multiple me's" (or for that matter, multiple you's). This just reflects the way that this space is connected to itself (it is said to be multiply connected versus simply connected). If one travels far enough in a particular direction, then one returns to the point of departure. This property is visually reflected in the fact that an inhabitant sees himself when looking in these particular directions. As a result, the inhabitant sees the sky "tiled" with copies of the fundamental domain and therefore sees himself layed out in a 3-D grid (the University of Minnesota's Geometry Center (1995) has produced a video The Shape of Space which gives animation of an inhabitant flying through a 3-torus, as well as related nonorientable 3-manifolds). As with the 2-torus, the 3-torus is flat and the geometry is Euclidean.

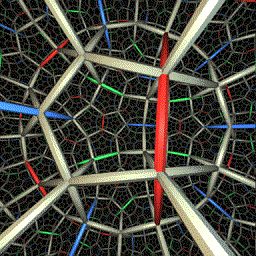
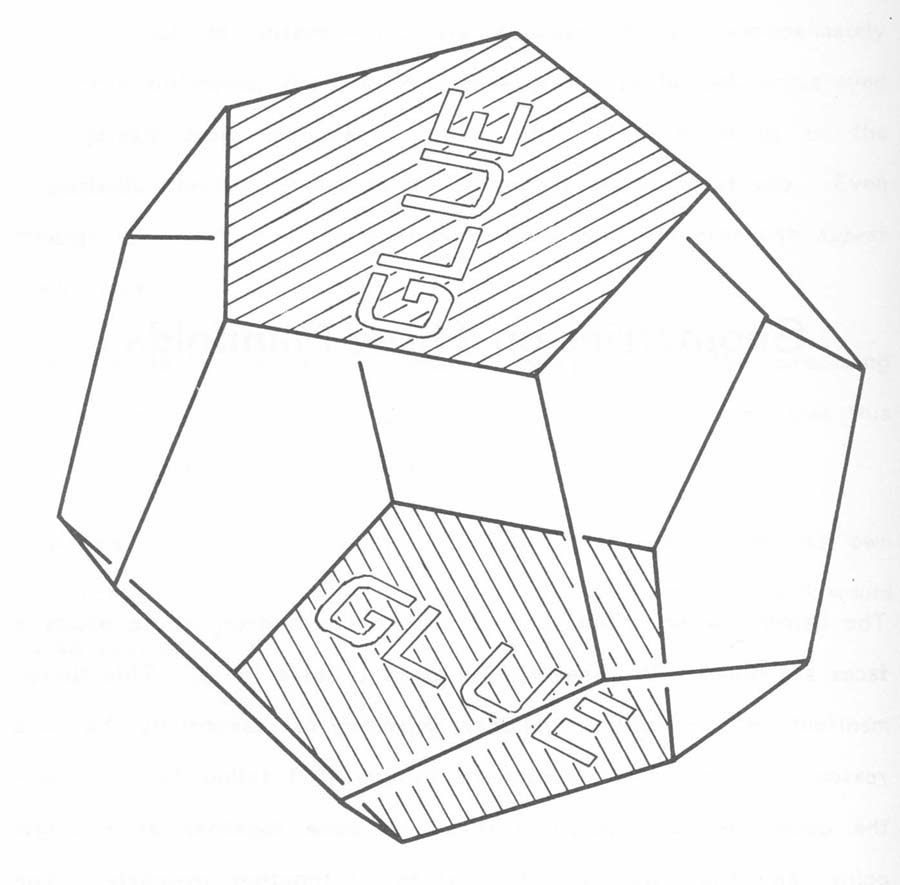
We now consider the view from inside infinite hyperbolic 3-space, H3. This description (which uses the projective or Klein model and represents geodesics as pieces of Euclidean straight lines, but distorts angles) is from Epstein and Gunn (1992, pp. 34-36). In this space, we see the sizes of objects decrease exponentially with distance. For example, if an object is moved 0.7 units of length further away, no matter how far away it is to begin with, its apparent size is halved. As a result, within a given distance, there is more volume (as opposed to the Euclidean case). We therefore see more when we look in a given direction. For example, we can see all of a "straight line" (to be precise, a "geodesic"), without turning our head (unlike our usual Euclidean experience). Figure 9 gives a picture which shows the view from within H3. In this figure, the space has been tiled with regular dodecahedra (it is impossible to tile Euclidean 3-space with these objects since the angles don't sum properly - however, the negative curvature of H3 allows such a tiling). This tiling lets us create compact hyperbolic 3-manifolds from dodecahedral fundamental domains. Such an example is the Seifert-Weber space of Figure 10. Of course, in both H3 and the Seifert-Weber space, the geometry is hyperbolic.

Although 2-manifolds can be classified by their genus, there does not yet exist a complete classification of 3-manifolds. The only homogeneous and isotropic 3-manifolds are the 3-sphere (S3), 3 dimensional Euclidean space (E3), and 3 dimensional hyperbolic space (H3) (Starkman 1998). If we try to enumerate all 3-manifolds, we find that, in a well defined mathematical sense, most of them are manifolds of negative curvature (Cornish et al. 1998). The fact that the (currently assumed) total amount of matter in the universe indicates a negative curvature universe, makes this a particularly interesting fact!

Figure 8. (a) The flat 3-torus is formed by conceptually joining opposite faces of a cube, as indicated by the colors (consider the front face as pink). When an inhabitant looks to the right, he sees the back of his own head. (b) In fact, the inhabitant sees the whole space tiled with images of himself!

Figure 9. The view inside of the hyperbolic space H3. The space has been tiled with regular dodecahedra, all of the same size. Notice how the sizes of these dodecahedra appear to decrease rapidly as a function of distance. Also notice how the nearby faces appear to meet at right angles, but the distant faces appear to meet at different angles. This image is from the Geometry Supercomputer Center's video Not Knot (1991).

Figure 10. The Seifert-Weber 3-manifold is constructed by tiling H3 with dodecahedra and conceptually joining opposite faces after giving them a 3/10 clockwise turn. This figure is from Weeks (1985).

Go to Section 5.