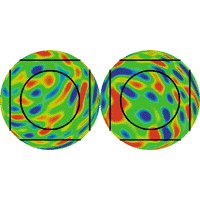TOPOLOGY, COSMOLOGY AND THE SHAPE OF SPACE
7. Empirical Detection of the Topology of the Universe
One way to detect the topology of the universe would be, as described
above, to look for multiple copies of ourselves. This could be done by
looking for, say, the Milky Way galaxy in distant images. Unfortunately,
on these scales, anything we can currently detect evolves too fast to be
recognized as it appeared billions of years ago (the amount of time it
would take light to reach us from our distant
self). Therefore we need a
less direct way to check the topology of the universe.
Some 200,000 years after the big bang, the universe became transparent to
radiation and a shower of light was released. This is seen today as the
Cosmic Microwave Background (CMB).
This radiation (first detected in the
early 1960's by Penzias and Wilson) is one of the strongest pieces of
evidence for the big bang.
 Today the CMB appears as a giant sphere of radiation with us at the center
of it (we are not in a special place - all locations see the CMB as a
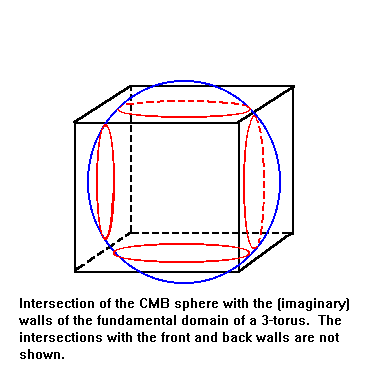
sphere of radiation with the observer at the center). If the universe is a
3-torus and if the radius of the CMB sphere is sufficiently large, then it
will not fit within the fundamental domain.
Today the CMB appears as a giant sphere of radiation with us at the center
of it (we are not in a special place - all locations see the CMB as a
sphere of radiation with the observer at the center). If the universe is a
3-torus and if the radius of the CMB sphere is sufficiently large, then it
will not fit within the fundamental domain.
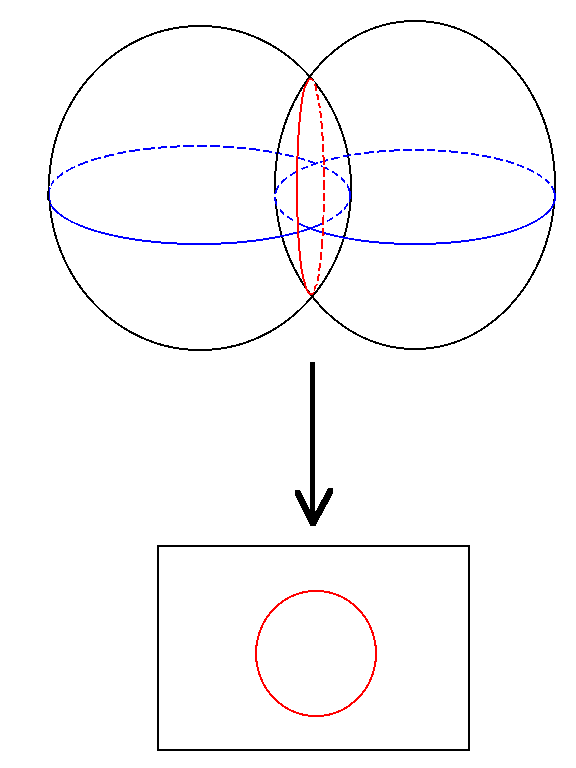
 In that case, we will see multiple copies of ourselves, each of which is at
a center of an image of the CMB sphere. Therefore we will see the spheres
intersect each other in circles.
In that case, we will see multiple copies of ourselves, each of which is at
a center of an image of the CMB sphere. Therefore we will see the spheres
intersect each other in circles.
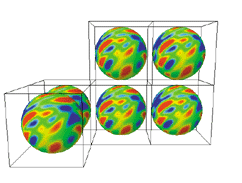
 In such a case, we could detect the topology of the universe by looking for
these circles in the sky. For example, if the universe is a giant 3-torus,
then we might see three pairs of circles in the sky, each resulting from
the intersection of the CMB sphere with itself in the principle directions
(the front-back, left-right, and top-bottom as described above).
In such a case, we could detect the topology of the universe by looking for
these circles in the sky. For example, if the universe is a giant 3-torus,
then we might see three pairs of circles in the sky, each resulting from
the intersection of the CMB sphere with itself in the principle directions
(the front-back, left-right, and top-bottom as described above).
In the 3-torus case, we have three possibilities:

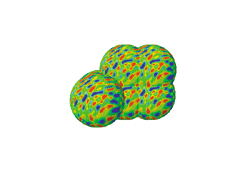
(From J.P. Luminet, G.D. Starkman, and J.R. Weeks (1999). Is Space Finite? Scientific American, April 1999, 90-97 [reference 9].)
These cases (in which the fundamental domain of the universe is large,
medium or small, respectively, as compared to the CMB sphere) lead to the
following circles of inhomogeneities (respectively):
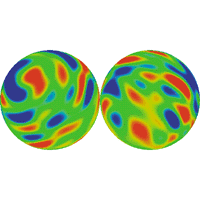
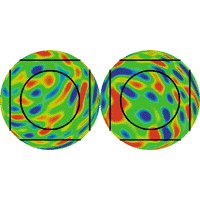

(From J.P. Luminet, G.D. Starkman, and J.R. Weeks (1999). Is Space Finite? Scientific American, April 1999, 90-97 [reference 9].)
It is the search for these "circles in the sky" that may lead
us to answer the fundamental question:
"What is the shape of the universe?"
Goto Section 8.